
Verlustfunktionen im Maschninellen Lernen
Verlustfunktionen im Maschninellen Lernen
Author: Christoph Würsch, ICE
Verlustfunktionen im ML
Table of Contents
- Optimierung von Modellen mittels Verlustfunktionen und Gradientenabstieg
- Verlustfunktionen für die Regression
- Verlustfunktionen für die Klassifikation
- Kontrastive Verlustfunktionen (Contrastive Losses)
- Adversariale Verlustfunktionen (Adversarial Losses)
- References
Dieser Artikel bietet einen umfassenden Überblick über Verlustfunktionen als zentrale Komponente der Modelloptimierung im Maschinellen Lernen. Er analysiert zunächst Funktionen für die Regression und beleuchtet deren unterschiedliche Robustheit gegenüber Ausreissern, wie beim Vergleich von MSE und MAE. Anschliessend werden Ansätze für die Klassifikation behandelt, die von Maximum-Margin-Methoden wie dem Hinge-Verlust bis zu probabilistischen Modellen mittels Kreuzentropie reichen. Weiterhin werden kontrastive Verluste für das selbst-überwachte Lernen von Datenrepräsentationen durch den Vergleich ähnlicher und unähnlicher Datenpunkte erläutert. Zuletzt stellt der Artikel adversariale Verluste vor, die das kompetitive Training von Generative Adversarial Networks (GANs) ermöglichen. Der Text verdeutlicht, dass die Wahl der Verlustfunktion eine kritische Designentscheidung ist, die die Leistung, Robustheit und das Verhalten eines Modells massgeblich beeinflusst.
1. Optimierung von Modellen mittels Verlustfunktionen und Gradientenabstieg
Im Rahmen des überwachten maschinellen Lernens ist das primäre Ziel, eine Funktion zu lernen, die Eingabedaten möglichst präzise auf zugehörige Zielwerte abbildet. Die Funktion wird durch einen Satz von Parametern (z.B. die Gewichte und Biases eines neuronalen Netzes) bestimmt. Um zu quantifizieren, wie gut das Modell mit den aktuellen Parametern diese Aufgabe erfüllt, wird eine Verlustfunktion (Loss Function) verwendet. Die Verlustfunktion misst die Diskrepanz oder den “Verlust” zwischen dem wahren Zielwert und der Vorhersage für ein einzelnes Datenbeispiel . Das übergeordnete Ziel des Trainingsprozesses ist es, die Parameter des Modells so zu optimieren, dass der durchschnittliche Verlust über den gesamten Trainingsdatensatz minimiert wird. Diese zu minimierende Zielfunktion (Objective Function), oft als bezeichnet, lautet typischerweise:
Hierbei bezeichnet den durchschnittlichen Gesamtverlust als Funktion der Parameter , während den Verlust für das einzelne Beispiel darstellt. Die Wahl einer geeigneten Verlustfunktion hängt massgeblich von der Art der Lernaufgabe ab. Wie in den folgenden Abschnitten detailliert beschrieben wird, verwendet man für Klassifikationsaufgaben andere Verlustfunktionen (z.B. Kreuzentropie, Hinge-Verlust) als für Regressionsaufgaben (z.B. Mittlerer Quadratischer Fehler, Mittlerer Absoluter Fehler) oder für komplexere Szenarien wie generative Modellierung (z.B. adversariale Verluste) oder das Lernen von Repräsentationen (z.B. kontrastive Verluste). Unabhängig von der spezifischen Wahl der Verlustfunktion benötigen wir ein algorithmisches Verfahren, um die optimalen Parameter zu finden, die die Zielfunktion minimieren:
Für einfache Modelle wie die lineare Regression existieren analytische Lösungen, aber für komplexe Modelle wie tiefe neuronale Netze ist typischerweise eine hochdimensionale, nicht-konvexe Funktion, für die analytische Lösungen nicht praktikabel sind. Hier kommen iterative Optimierungsverfahren ins Spiel.
1.1. Das Gradientenabstiegsverfahren (Gradient Descent)
Das bei weitem am häufigsten verwendete Optimierungsverfahren im maschinellen Lernen, insbesondere im Deep Learning, ist das Gradientenabstiegsverfahren (Gradient Descent). Die Grundidee ist einfach: Man startet mit einer anfänglichen Schätzung der Parameter und bewegt sich dann iterativ in kleinen Schritten in die Richtung, die den Wert der Verlustfunktion am stärksten reduziert.
Herleitung: Wir möchten die Parameter so ändern, dass der Wert der Zielfunktion sinkt. Angenommen, wir befinden uns beim Parametervektor im -ten Iterationsschritt. Wir suchen eine kleine Änderung , sodass gilt. Mittels einer Taylor-Entwicklung erster Ordnung können wir in der Nähe von approximieren:
Hierbei ist der Gradientenvektor der Zielfunktion bezüglich der Parameter , ausgewertet an der Stelle . Der Gradient zeigt in die Richtung des steilsten Anstiegs der Funktion an der Stelle . Damit gilt, muss der zweite Term in Gl. \eqref{eq:taylor_expansion_L} negativ sein:
Um den Wert von möglichst schnell zu reduzieren, suchen wir die Richtung , die bei einer festen (kleinen) Schrittlänge den Wert des Skalarprodukts minimiert. Das Skalarprodukt wird minimal (am negativsten), wenn der Winkel zwischen den Vektoren und gleich ist, d.h., wenn in die genau entgegengesetzte Richtung des Gradienten zeigt. Wir wählen daher die Aktualisierungsrichtung als den negativen Gradienten:
Hier ist ein kleiner positiver Skalar, der als Lernrate (Learning Rate) bezeichnet wird. Die Lernrate steuert die Schrittweite bei jedem Aktualisierungsschritt. Eine zu grosse Lernrate kann dazu führen, dass der Algorithmus über das Minimum hinausschiesst und divergiert, während eine zu kleine Lernrate die Konvergenz stark verlangsamt.
Die Update-Regel: Kombiniert man die aktuelle Parameterschätzung mit der Änderung , ergibt sich die iterative Update-Regel des Gradientenabstiegs:
Dieser Schritt wird wiederholt, bis ein Konvergenzkriterium erfüllt ist, z.B. wenn der Gradient sehr klein wird (), die Änderung der Parameter oder des Verlusts unter einen Schwellenwert fällt, oder eine maximale Anzahl von Iterationen erreicht ist.
Algorithmus (Allgemeine Form):
- Initialisiere die Parameter (z.B. zufällig).
- Wiederhole für bis Konvergenz: a. Berechne den Gradienten der Zielfunktion: . b. Aktualisiere die Parameter: .
- Gebe die optimierten Parameter zurück.
1.2. Varianten des Gradientenabstiegs
Die Berechnung des exakten Gradienten erfordert gemäss Gl. \eqref{eq:objective_function_L} die Berechnung des Verlusts und seines Gradienten für jedes einzelne Beispiel im Trainingsdatensatz :
Für sehr grosse Datensätze (z.B. Millionen von Bildern) ist die Berechnung dieses vollständigen Gradienten in jedem Iterationsschritt extrem rechenaufwändig und möglicherweise unpraktikabel. Aus diesem Grund wurden verschiedene Varianten des Gradientenabstiegs entwickelt.
1.2.1. Batch Gradient Descent (BGD)
Erklärung: Dies ist die Standardvariante, die oben beschrieben wurde. Der Gradient wird über den gesamten Trainingsdatensatz berechnet, bevor ein einziger Parameterschritt durchgeführt wird.
Formel (Update):
Vorteile:
- Der Gradient ist eine exakte Schätzung des wahren Gradienten der Zielfunktion .
- Die Konvergenz ist oft stabil und direkt auf ein lokales (bei konvexen Problemen globales) Minimum gerichtet.
Nachteile:
- Sehr langsam und rechenintensiv für grosse Datensätze, da alle Daten für jeden Schritt verarbeitet werden müssen.
- Möglicherweise nicht durchführbar, wenn der Datensatz nicht in den Speicher passt.
- Kann in flachen lokalen Minima stecken bleiben.
1.2.2. Stochastic Gradient Descent (SGD)
Erklärung: Beim Stochastischen Gradientenabstieg wird der Gradient für die Parameteraktualisierung basierend auf nur einem einzigen, zufällig ausgewählten Trainingsbeispiel in jedem Schritt geschätzt.
Formel (Update für Beispiel ):
Innerhalb einer Trainingsepoche (ein Durchlauf durch den gesamten Datensatz) werden also Parameter-Updates durchgeführt.
Vorteile:
- Deutlich schnellere Updates ( Updates pro Epoche vs. 1 bei BGD).
- Geringer Speicherbedarf pro Update (nur ein Beispiel).
- Die hohe Varianz (“Rauschen”) im Gradienten kann helfen, aus flachen lokalen Minima zu entkommen und potenziell bessere Minima zu finden.
- Ermöglicht Online-Lernen (Modellaktualisierung bei Eintreffen neuer Daten).
Nachteile:
- Hohe Varianz der Gradientenschätzung führt zu stark oszillierendem Konvergenzpfad.
- Konvergiert nicht exakt zum Minimum, sondern oszilliert typischerweise darum herum (es sei denn, die Lernrate wird über die Zeit reduziert).
- Verliert Effizienzvorteile durch vektorisierte Operationen auf moderner Hardware (GPUs).
1.2.3. Mini-Batch Gradient Descent (MBGD)
Erklärung: Dies ist der am häufigsten verwendete Kompromiss zwischen BGD und SGD. Der Gradient wird über einen kleinen, zufällig ausgewählten Teildatensatz, den sogenannten Mini-Batch der Grösse (wobei ), berechnet. Typische Batch-Grössen liegen im Bereich von bis .
Formel (Update für Mini-Batch ):
Eine Epoche besteht aus Updates.
Vorteile:
- Reduziert die Varianz der Gradientenschätzung im Vergleich zu SGD, was zu stabilerer Konvergenz führt.
- Nutzt die Vorteile der Vektorisierung und parallelen Verarbeitung auf GPUs effizient aus.
- Schneller als BGD und oft stabiler/effizienter als reines SGD.
Nachteile:
- Einführung eines neuen Hyperparameters (Batch-Grösse ), der abgestimmt werden muss.
- Der Gradient ist immer noch eine Schätzung (weniger verrauscht als SGD, aber nicht exakt wie BGD).
Die hier vorgestellten Varianten des Gradientenabstiegs bilden die Grundlage für die Optimierung der meisten modernen Modelle des maschinellen Lernens. Aufbauend darauf wurden zahlreiche Weiterentwicklungen vorgeschlagen, um die Konvergenzgeschwindigkeit und -stabilität weiter zu verbessern. Dazu gehören Techniken wie die Verwendung von Momentum (um Oszillationen zu dämpfen und die Konvergenz zu beschleunigen) oder adaptive Lernratenverfahren (wie AdaGrad, RMSprop und Adam), die die Lernrate für jeden Parameter individuell anpassen. Die spezifische Berechnung des Gradienten hängt natürlich von der gewählten Verlustfunktion und der Architektur des Modells ab. Für neuronale Netze wird dieser Gradient effizient mittels des Backpropagation-Algorithmus berechnet, welcher im Wesentlichen die Kettenregel der Differentialrechnung anwendet. Die Details der spezifischen Verlustfunktionen für verschiedene Aufgaben werden in den folgenden Abschnitten behandelt.
2. Verlustfunktionen für die Regression
Bei Regressionsproblemen im überwachten Lernen ist das Ziel, eine kontinuierliche Zielvariable basierend auf Eingabemerkmalen vorherzusagen. Ein Regressionsmodell lernt eine Funktion, die eine Vorhersage für einen gegebenen Input liefert. Die Verlustfunktion spielt hierbei die entscheidende Rolle, die Diskrepanz oder den Fehler zwischen dem wahren Wert und dem vorhergesagten Wert zu quantifizieren. Das Ziel des Trainings ist es, die Parameter des Modells so anzupassen, dass der durchschnittliche Verlust über den Trainingsdatensatz minimiert wird. Die Wahl der Verlustfunktion beeinflusst nicht nur die Konvergenz des Trainingsprozesses, sondern auch die Eigenschaften der resultierenden Vorhersagen (z.B. ob das Modell tendenziell den Mittelwert oder den Median vorhersagt) und die Robustheit des Modells gegenüber Ausreissern in den Daten. Wir verwenden die folgende Notation: ist der wahre Wert für das -te Beispiel, ist der vom Modell vorhergesagte Wert, und ist die Anzahl der Beispiele im Datensatz. Der Fehler oder das Residuum für ein Beispiel ist .
2.1. Mittlerer Quadratischer Fehler (Mean Squared Error, MSE / L2-Verlust)
Der Mittlere Quadratische Fehler (MSE), auch L2-Verlust genannt, ist die am häufigsten verwendete Verlustfunktion für Regressionsprobleme.
Erklärung: MSE berechnet den Durchschnitt der quadrierten Differenzen zwischen den wahren und den vorhergesagten Werten. Durch das Quadrieren werden grössere Fehler überproportional stark bestraft. Dies macht MSE sehr empfindlich gegenüber Ausreissern.
Formel:
Für einen einzelnen Datenpunkt wird der Verlust oft als betrachtet.
Herleitung/Motivation: MSE ergibt sich natürlich aus der Maximum-Likelihood-Schätzung (MLE), wenn angenommen wird, dass die Fehler unabhängig und identisch normalverteilt (Gaussverteilung) mit Mittelwert Null und konstanter Varianz sind. Unter dieser Annahme maximiert die Minimierung des MSE die Plausibilität der Modellparameter gegeben die Daten. Mathematisch ist MSE attraktiv, da die Funktion konvex und glatt (unendlich oft differenzierbar) ist, was die Optimierung mit gradientenbasierten Methoden erleichtert. Die Ableitung nach ist einfach . Modelle, die mit MSE trainiert werden, lernen tendenziell, den bedingten Mittelwert von gegeben vorherzusagen.
Eigenschaften und Herausforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Grundidee | Minimiere den Durchschnitt der quadrierten Fehler. |
| Formel (pro Punkt) | . |
| Ableitung (nach ) | . |
| Vorteile |
|
| Nachteile/ Herausforderungen |
|
| Use Cases | Standard-Verlustfunktion für viele Regressionsalgorithmen (z.B. Lineare Regression, Neuronale Netze), wenn keine starken Ausreisser erwartet werden oder der Mittelwert von Interesse ist. |
2.2. Mittlerer Absoluter Fehler (Mean Absolute Error, MAE / L1-Verlust)
Der Mittlere Absolute Fehler (MAE), auch L1-Verlust genannt, ist eine Alternative zu MSE, die robuster gegenüber Ausreissern ist.
Erklärung: MAE berechnet den Durchschnitt der absoluten Differenzen zwischen den wahren und den vorhergesagten Werten. Da die Fehler linear und nicht quadratisch gewichtet werden, haben Ausreisser einen geringeren Einfluss auf den Gesamtverlust als bei MSE.
Formel:
Für einen einzelnen Datenpunkt ist der Verlust .
Herleitung/Motivation: MAE entspricht der MLE, wenn angenommen wird, dass die Fehler einer Laplace-Verteilung folgen. Ein Modell, das trainiert wird, um MAE zu minimieren, lernt, den bedingten Median von gegeben vorherzusagen. Der Median ist bekanntermassen robuster gegenüber Ausreissern als der Mittelwert. Ein Nachteil ist, dass die MAE-Funktion am Punkt (Fehler ) nicht differenzierbar ist (die Ableitung springt von -1 auf +1). In der Praxis verwendet man Subgradienten (z.B. 0 oder ) oder glättet die Funktion nahe null. Die Ableitung nach ist .
Eigenschaften und Herausforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Grundidee | Minimiere den Durchschnitt der absoluten Fehler. |
| Formel (pro Punkt) | $ |
| Ableitung (nach ) | (definiert als 0 oder bei ). |
| Vorteile |
|
| Nachteile/ Herausforderungen |
|
| Use Cases | Regression bei Vorhandensein von Ausreissern, Vorhersage des Medians, Situationen, in denen grosse Fehler nicht überproportional bestraft werden sollen. |
2.3. Huber-Verlust
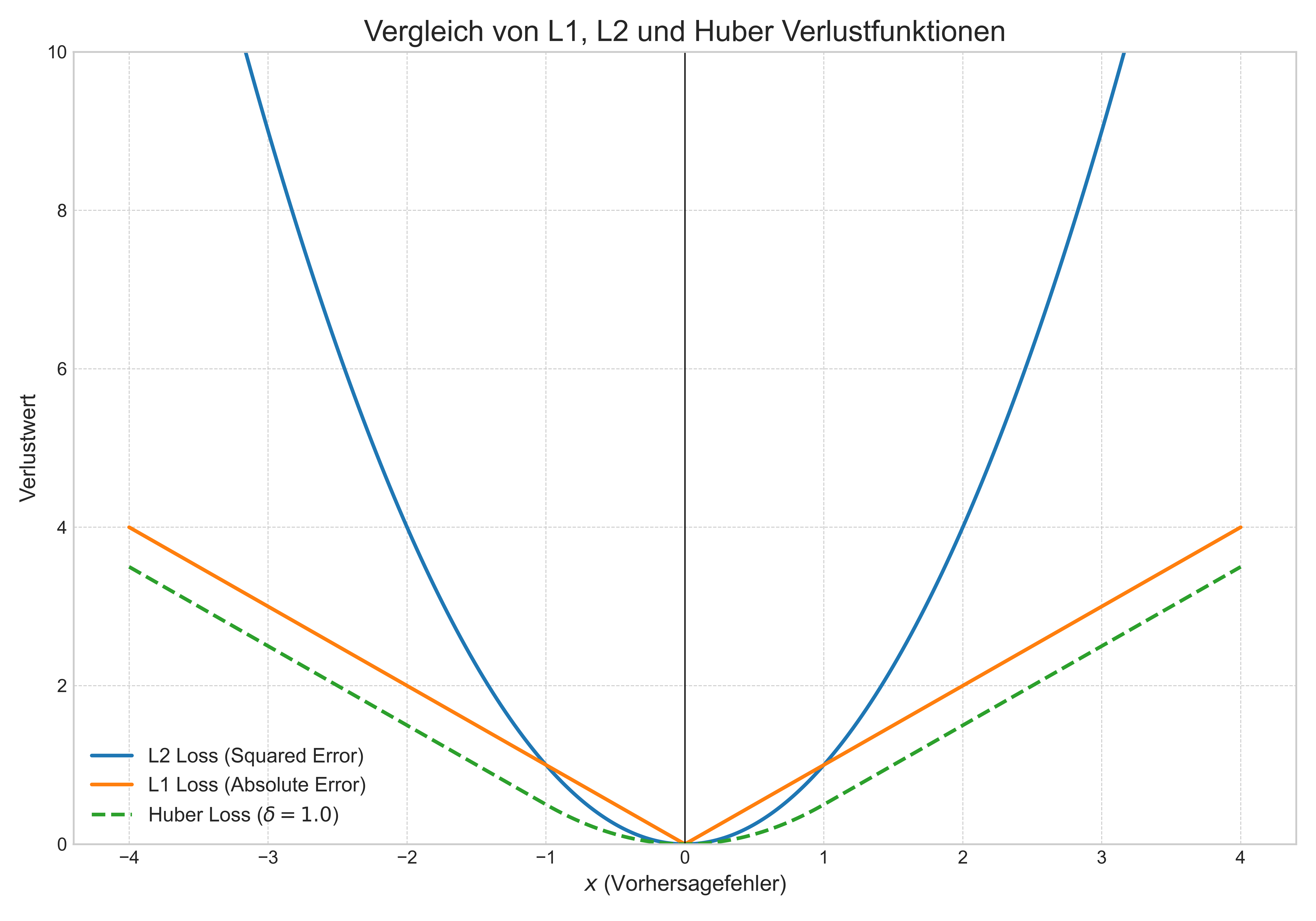
Der Huber-Verlust ist eine hybride Verlustfunktion, die versucht, die Vorteile von MSE und MAE zu kombinieren.
Erklärung: Der Huber-Verlust verhält sich wie MSE für kleine Fehler (innerhalb eines Schwellenwerts ) und wie MAE (linear) für grosse Fehler. Der Parameter steuert den Übergangspunkt. Dadurch ist der Huber-Verlust weniger empfindlich gegenüber Ausreissern als MSE, aber immer noch differenzierbar am Nullpunkt (im Gegensatz zu MAE).
Formel: Für einen einzelnen Fehler :
Der Gesamtverlust ist der Durchschnitt über alle Datenpunkte.
Motivation: Ziel ist es, die Robustheit von MAE für grosse Fehler mit der Effizienz und Glattheit von MSE für kleine Fehler zu verbinden. Die Funktion ist stetig differenzierbar.
Eigenschaften und Herausforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Grundidee | Quadratischer Verlust für kleine Fehler, linearer Verlust für grosse Fehler. |
| Formel (pro Punkt, ) | Siehe Gl. \eqref{eq:huber_loss}. |
| Ableitung (nach , für ) | $\begin{cases} - \varepsilon & \text{für } |
| Parameter | (Schwellenwert für den Übergang). |
| Vorteile |
|
| Nachteile/ Herausforderungen |
|
| Use Cases | Robuste Regression, wenn Ausreisser erwartet werden, aber die Glattheit von MSE wünschenswert ist. Oft in Verstärkungslernen (Reinforcement Learning) verwendet. |
2.4. Log-Cosh-Verlust
Der Log-Cosh-Verlust ist eine weitere glatte Verlustfunktion, die sich ähnlich wie MAE verhält, aber überall zweimal differenzierbar ist.
Erklärung: Er basiert auf dem Logarithmus des hyperbolischen Kosinus des Fehlers. Für kleine Fehler approximiert den quadratischen Fehler , während es für grosse Fehler dem absoluten Fehler ähnelt.
Formel:
(Beachte: )
Motivation: Ziel ist es, eine Verlustfunktion zu haben, die die Robustheitseigenschaften von MAE/Huber besitzt, aber sehr glatt ist (unendlich oft differenzierbar), was für manche Optimierungsalgorithmen (z.B. solche, die zweite Ableitungen nutzen) vorteilhaft sein kann.
Eigenschaften und Herausforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Grundidee | Glatte (zweimal differenzierbare) Annäherung an MAE. |
| Formel (pro Punkt) | . |
| Ableitung (nach ) | . |
| Vorteile |
|
| Nachteile/ Herausforderungen |
|
| Use Cases | Robuste Regression, wenn Glattheit (zweite Ableitung) wichtig ist. Alternative zu Huber, wenn keine Parameterabstimmung gewünscht ist. |
2.5. Quantil-Verlust (Pinball Loss)
Der Quantil-Verlust, auch Pinball Loss genannt, wird verwendet, um bedingte Quantile (anstelle des Mittelwerts oder Medians) der Zielvariablen vorherzusagen.
Erklärung: Quantilregression ermöglicht es, verschiedene Punkte der bedingten Verteilung von zu modellieren, z.B. das 10., 50. (Median) oder 90. Perzentil. Der Quantil-Verlust ist asymmetrisch und bestraft Über- und Unterschätzungen unterschiedlich, abhängig vom Zielquantil .
Formel: Für einen Fehler und ein Zielquantil :
Dies kann auch kompakt als geschrieben werden. Der Gesamtverlust ist der Durchschnitt über alle Datenpunkte.
Motivation: Für ist der Verlust , was äquivalent zu MAE ist (Minimierung führt zur Vorhersage des Medians). Für werden Unterschätzungen () stärker bestraft als Überschätzungen (), was das Modell dazu bringt, höhere Quantile vorherzusagen. Für ist es umgekehrt. Dies ist nützlich, um Unsicherheitsintervalle zu schätzen oder Risiken zu modellieren.
Eigenschaften und Herausforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Grundidee | Asymmetrische Bestrafung von Fehlern zur Vorhersage spezifischer bedingter Quantile. |
| Formel (pro Punkt, ) | . |
| Parameter | (Zielquantil). |
| Vorteile |
|
| Nachteile/ Herausforderungen |
|
| Use Cases | Quantilregression, Schätzung von Vorhersageintervallen, Risikomodellierung (z.B. Value-at-Risk), Ökonometrie, überall dort, wo die gesamte Verteilung von Interesse ist. |
2.6 Die verallgemeinerte Verlustfunktion
T. Barron stellt eine verallgemeinerte Verlustfunktion vor, die eine Obermenge vieler gebräuchlicher robuster Verlustfunktionen darstellt. Durch die Anpassung eines einzigen, kontinuierlich veränderbaren Parameters kann diese Funktion so eingestellt werden, dass sie mehreren traditionellen Verlustfunktionen entspricht oder eine breitere Familie von Funktionen modelliert. Dies ermöglicht die Verallgemeinerung von Algorithmen, die auf einer festen robusten Verlustfunktion aufbauen, indem ein neuer Hyperparameter für die “Robustheit” eingeführt wird. Dieser kann justiert oder durch Techniken wie Annealing optimiert werden, um die Leistung zu verbessern.
Die grundlegende Form der Verlustfunktion ist wie folgt definiert:
Hierbei ist ein Formparameter, der die Robustheit der Verlustfunktion steuert, und ist ein Skalierungsparameter, der die Breite des quadratischen Bereichs der Funktion in der Nähe von bestimmt.
Spezialfälle und Grenzwerte
Obwohl die Funktion für nicht definiert ist, nähert sie sich im Grenzwert dem L2-Verlust (quadratischer Fehler) an:
Für ergibt sich eine geglättete Form des L1-Verlusts, die oft als Charbonnier- oder Pseudo-Huber-Verlust bezeichnet wird:
Diese Funktion verhält sich in der Nähe des Ursprungs wie der L2-Verlust und für größere Werte wie der L1-Verlust.
Die Ausdruckskraft der Funktion wird besonders deutlich, wenn nicht-positive Werte für den Formparameter betrachtet werden. Obwohl nicht definiert ist, kann der Grenzwert für gebildet werden:
Dies entspricht dem Cauchy- (oder Lorentz-) Verlust.
Durch Setzen von wird der Geman-McClure-Verlust reproduziert:
Im Grenzwert für ergibt sich der Welsch- (oder Leclerc-) Verlust:
Unter Berücksichtigung dieser Spezialfälle kann die vollständige, stückweise definierte Verlustfunktion formuliert werden, welche die hebbaren Singularitäten bei und sowie den Grenzwert bei explizit behandelt:
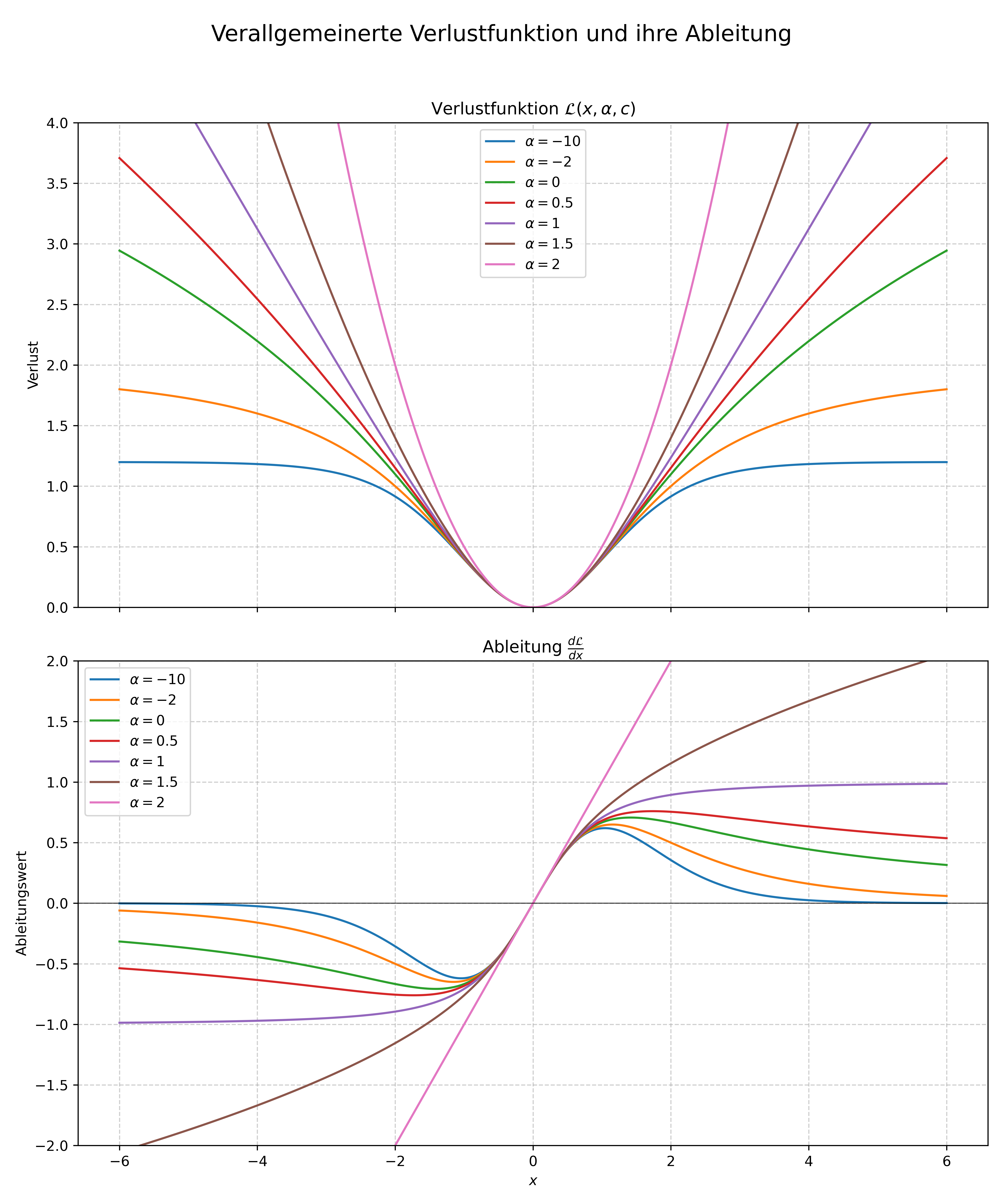
Wie gezeigt wurde, umfasst diese Funktion eine Vielzahl bekannter robuster Verlustfunktionen.
Ableitung und Interpretation
Für gradientenbasierte Optimierungsverfahren ist die Ableitung der Verlustfunktion nach von entscheidender Bedeutung:
Die Form der Ableitung gibt Aufschluss darüber, wie der Parameter das Verhalten bei der Minimierung mittels Gradientenabstieg beeinflusst.
-
Für alle -Werte: Ist der Fehler (Residuum) klein (), ist die Ableitung annähernd linear. Der Einfluss eines kleinen Residuums ist also immer proportional zu seiner Größe.
-
Für (L2-Verlust): Der Betrag der Ableitung wächst linear mit dem Residuum. Größere Fehler haben einen entsprechend größeren Einfluss auf die Anpassung.
-
Für (Geglätteter L1-Verlust): Der Betrag der Ableitung sättigt bei einem konstanten Wert von , wenn größer als wird. Der Einfluss eines Fehlers nimmt also nie ab, überschreitet aber auch nie einen festen Betrag.
-
Für (Robuste Verluste): Der Betrag der Ableitung beginnt zu sinken, wenn größer als wird. Man spricht hier von einer “redescending” Einflussfunktion. Das bedeutet, dass der Einfluss eines Ausreißers mit zunehmendem Residuum geringer wird. Je negativer wird, desto stärker wird dieser Effekt. Für wird ein Ausreißer mit einem Residuum größer als fast vollständig ignoriert.
Eine weitere Interpretation ergibt sich aus der Perspektive statistischer Mittelwerte. Die Minimierung des L2-Verlusts () entspricht der Schätzung des arithmetischen Mittels. Die Minimierung des L1-Verlusts () ähnelt der Schätzung des Medians. Die Minimierung des Verlusts für ist äquivalent zur lokalen Modus-Suche. Werte für zwischen diesen Extremen können als eine glatte Interpolation zwischen diesen drei Arten von Mittelwertschätzungen betrachtet werden.
2.7. Vergleich von Regressions-Verlustfunktionen
Die Wahl der Verlustfunktion in der Regression ist ein wichtiger Aspekt des Modelldesigns. MSE ist der Standard aufgrund seiner mathematischen Einfachheit und Verbindung zur Gauss-Annahme, aber seine Empfindlichkeit gegenüber Ausreissern ist ein signifikanter Nachteil in vielen realen Anwendungen. MAE bietet Robustheit, opfert aber die Differenzierbarkeit am Minimum. Huber und Log-Cosh stellen Kompromisse dar, die Robustheit mit Glattheit verbinden, wobei Huber einen expliziten Parameter benötigt. Der Quantil-Verlust erweitert den Fokus von zentralen Tendenzmassen (Mittelwert, Median) auf die gesamte bedingte Verteilung und ist unerlässlich für Aufgaben wie die Schätzung von Unsicherheitsintervallen. Die Entscheidung sollte basierend auf den Eigenschaften der Daten (insbesondere dem Vorhandensein von Ausreissern) und dem spezifischen Ziel der Regressionsanalyse getroffen werden (z.B. Vorhersage des Durchschnitts, des wahrscheinlichsten Werts oder eines bestimmten Quantils). Tabelle 1 fasst die Hauptmerkmale zusammen.
Tabelle 1: Vergleich von Regressions-Verlustfunktionen
| Verlustfunktion | Formel (pro Punkt, ) | Optimalvorhersage | Robustheit ggü. Ausreissern | Differenzierbarkeit | Hauptanwendung |
|---|---|---|---|---|---|
| MSE (L2) | Bedingter Mittelwert | Gering | Ja (glatt) | Standardregression, Gauss-Rauschen | |
| MAE (L1) | $ | \varepsilon | $ | Bedingter Median | Hoch |
| Huber | $\begin{cases} \frac{1}{2}\varepsilon^2 & |\varepsilon | \le\delta \ \delta(|\varepsilon | -\frac{1}{2}\delta) & |\varepsilon | >\delta \end{cases}$ | Kompromiss Mittelwert/Median |
| Log-Cosh | Ähnlich Median | Mittel-Hoch | Ja (glatt) | Robuste Regression (glatt) | |
| Quantil (Pinball) | Bedingtes -Quantil | Hoch | Nein (bei ) | Quantilregression, Unsicherheitsschätzung | |
| Hinweis: . Robustheit ist relativ. Differenzierbarkeit bezieht sich auf die Stetigkeit der ersten Ableitung. |
3. Verlustfunktionen für die Klassifikation
Beim überwachten Lernen für die Klassifikation ist das Ziel, eine Abbildung von einem Eingaberaum (z.B. ) in einen diskreten Ausgaberaum , der die Klassenlabels repräsentiert, zu lernen. Für eine gegebene Eingabe erzeugt das Modell eine Vorhersage, die ein Rohwert (Score) , eine Wahrscheinlichkeitsverteilung oder ein direktes Klassenlabel sein kann. Eine Verlustfunktion, oder , quantifiziert die Kosten (den „Verlust“), die entstehen, wenn das wahre Label ist und die Vorhersage bzw. aus abgeleitet ist. Das Ziel während des Trainings ist typischerweise die Minimierung des durchschnittlichen Verlusts über den Trainingsdatensatz. Obwohl das ultimative Ziel bei der Klassifikation oft die Minimierung der Anzahl von Fehlklassifikationen ist (gemessen durch den Null-Eins-Verlust), ist diese Verlustfunktion nicht konvex und lässt sich nur schwer direkt mit gradientenbasierten Methoden optimieren. Daher werden verschiedene Surrogat-Verlustfunktionen (auch Ersatz-Verlustfunktionen genannt) verwendet, die typischerweise konvex und differenzierbar sind und als Annäherungen an den Null-Eins-Verlust dienen.
Wir betrachten hauptsächlich zwei gängige Konventionen für Labels:
- Binäre Klassifikation mit : Hier gibt das Modell oft einen reellwertigen Score aus. Das Vorzeichen von bestimmt typischerweise die vorhergesagte Klasse , und der Betrag kann als Konfidenz interpretiert werden.
- Binäre/Multiklassen-Klassifikation mit Wahrscheinlichkeiten: Hier wird das wahre Label oft als ganze Zahl oder als One-Hot-Vektor dargestellt. Das Modell gibt eine Wahrscheinlichkeit (für binär, ) oder eine Wahrscheinlichkeitsverteilung aus, wobei . Der Score oder Vektor repräsentiert oft die Werte vor der Aktivierungsfunktion (Logits), bevor eine Funktion wie Sigmoid oder Softmax angewendet wird.
Im Folgenden untersuchen wir die wichtigsten Verlustfunktionen für die Klassifikation.
3.1. Null-Eins-Verlust (Zero-One Loss)
Der Null-Eins-Verlust misst direkt den Klassifikationsfehler. Er weist einer Fehlklassifikation einen Verlust von 1 und einer korrekten Klassifikation einen Verlust von 0 zu.
Formel: Mit vorhergesagtem Label :
Mit Score für (unter Annahme der Vorhersage ):
Hier ist die Indikatorfunktion, die 1 zurückgibt, wenn die Bedingung wahr ist, und 0 sonst. Der Term ist genau dann positiv, wenn die Vorhersage das korrekte Vorzeichen hat.
Herleitung: Diese Verlustfunktion ist definitorisch und spiegelt direkt das Ziel der Minimierung von Fehlklassifikationen wider.
Eigenschaften und Anwendungsfälle:
| Eigenschaft | Beschreibung |
|---|---|
| Vorteile |
|
| Nachteile |
|
| Use Cases | Hauptsächlich zur Evaluierung der finalen Modellleistung, nicht zur direkten Optimierung während des Trainings. Andere Verlustfunktionen dienen als Surrogat. |
3.2. Hinge-Verlust (Hinge Loss)
Der Hinge-Verlust wird hauptsächlich in Verbindung mit Support-Vektor-Maschinen (SVMs) und der Maximum-Margin-Klassifikation verwendet. Er bestraft Vorhersagen, die falsch sind oder korrekt sind, aber innerhalb der Marge liegen.
Formel: (für und Score )
Der Term wird oft als Margin-Score bezeichnet. Der Verlust ist null, wenn der Punkt korrekt mit einer Marge von mindestens 1 klassifiziert wird (). Andernfalls steigt der Verlust linear mit dem negativen Margin-Score.
Herleitung: Der Hinge-Verlust ergibt sich aus der Formulierung von Soft-Margin-SVMs. Ziel ist es, eine Hyperebene zu finden, sodass für Schlupfvariablen gilt. Die Minimierung einer Kombination aus der Margengrösse () und der Gesamtsumme der Schlupfvariablen führt zur Minimierung von , wobei und der zweite Term den Hinge-Verlust verwendet.
Eigenschaften und Anwendungsfälle:
| Eigenschaft | Beschreibung |
|---|---|
| Vorteile |
|
| Nachteile |
|
| Use Cases | Standard-Verlustfunktion für das Training von linearen SVMs und Kernel-SVMs. |
3.3. Logistischer Verlust (Binäre Kreuzentropie)
Der Logistische Verlust, auch bekannt als Log-Verlust oder Binäre Kreuzentropie (Binary Cross-Entropy), wird häufig in der Logistischen Regression und in neuronalen Netzen für die binäre Klassifikation verwendet. Er leitet sich vom Prinzip der Maximum-Likelihood-Schätzung unter Annahme einer Bernoulli-Verteilung für die Labels ab.
Formel: Es gibt zwei gebräuchliche Formen, abhängig von der Label- und Ausgabedarstellung.
- Labels , Modellausgabe (oft wobei der Logit ist):
- Labels , Modellausgabe Score :
Diese Form ist äquivalent zur ersten, wenn und die Labels entsprechend abgebildet werden (z.B. ).
Herleitung (Maximum Likelihood): Angenommen, die bedingte Wahrscheinlichkeit des Klassenlabels folgt einer Bernoulli-Verteilung: für . Gegeben sei ein Datensatz . Die Likelihood (Plausibilität) ist . Die Maximierung der Likelihood ist äquivalent zur Minimierung der negativen Log-Likelihood (NLL):
Der Verlust für ein einzelnes Beispiel ist genau der Logistische Verlust / Binäre Kreuzentropie aus Gl. \eqref{eq:log_loss_prob_de}.
Eigenschaften und Anwendungsfälle:
| Eigenschaft | Beschreibung |
|---|---|
| Vorteile |
|
| Nachteile |
|
| Use Cases | Training von Logistischen Regressionsmodellen, Standardwahl für binäre Klassifikationsaufgaben in neuronalen Netzen (oft gepaart mit einer finalen Sigmoid-Aktivierung). |
3.4. Kategorische Kreuzentropie (Categorical Cross-Entropy)
Die Kategorische Kreuzentropie ist die Verallgemeinerung des Logistischen Verlusts auf Multiklassen-Klassifikationsprobleme ( Klassen).
Formel: Erfordert wahre Labels im One-Hot-kodierten Format (wobei für die wahre Klasse und für ) und Modellausgaben als Wahrscheinlichkeitsverteilung , wobei und . Typischerweise ist , wobei der Vektor der Logits ist.
Da one-hot ist, überlebt nur der Term, der der wahren Klasse (wo ) entspricht:
Das bedeutet, der Verlust bestraft das Modell basierend auf der Wahrscheinlichkeit, die es der korrekten Klasse zuweist.
Herleitung (Maximum Likelihood): Angenommen, die bedingte Wahrscheinlichkeit des Klassenlabels folgt einer Multinoulli- (Kategorischen) Verteilung: . Für eine One-Hot-kodierte Beobachtung (mit ) ist die Wahrscheinlichkeit . Die negative Log-Likelihood für ein einzelnes Beispiel ist , was genau der Kategorischen Kreuzentropie entspricht.
Eigenschaften und Anwendungsfälle:
| Eigenschaft | Beschreibung |
|---|---|
| Vorteile |
|
| Nachteile |
|
| Use Cases | Standard-Verlustfunktion für Multiklassen-Klassifikationsprobleme, insbesondere in neuronalen Netzen (typischerweise gepaart mit einer finalen Softmax-Aktivierungsschicht). |
3.5. Quadratischer Hinge-Verlust (Squared Hinge Loss)
Dies ist eine Variante des Hinge-Verlusts, bei der die Strafe quadratisch statt linear ist.
Formel: (für und Score )
Herleitung: Eine direkte Modifikation des Standard-Hinge-Verlusts, bei der der Term, der die Margin-Verletzung darstellt, quadriert wird.
Eigenschaften und Anwendungsfälle:
| Eigenschaft | Beschreibung |
|---|---|
| Vorteile |
|
| Nachteile |
|
| Use Cases | Eine Alternative zum Standard-Hinge-Verlust bei SVMs (manchmal als L2-SVM bezeichnet). Kann auch in anderen linearen Modellen oder neuronalen Netzen verwendet werden. |
3.6. Exponentieller Verlust (Exponential Loss)
Der Exponentielle Verlust weist fehlklassifizierten Punkten eine exponentiell ansteigende Strafe basierend auf ihrem Margin-Score zu. Er ist am bekanntesten durch den AdaBoost-Algorithmus.
Formel: (für und Score )
Herleitung: AdaBoost kann als ein vorwärts gerichteter stufenweiser additiver Modellierungsalgorithmus hergeleitet werden, der die exponentielle Verlustfunktion optimiert. In jeder Stufe wird ein schwacher Lerner hinzugefügt, um den exponentiellen Gesamtverlust des Ensembles zu minimieren.
Eigenschaften und Anwendungsfälle:
| Eigenschaft | Beschreibung |
|---|---|
| Vorteile |
|
| Nachteile |
|
| Use Cases | Hauptsächlich im Kontext von Boosting-Algorithmen verwendet, insbesondere AdaBoost. |
3.7. Vergleich und Zusammenfassung
Die Wahl der richtigen Verlustfunktion hängt vom spezifischen Algorithmus, der gewünschten Ausgabe (Scores vs. Wahrscheinlichkeiten), den Anforderungen an die Robustheit und den rechnerischen Überlegungen ab. Während der Null-Eins-Verlust das wahre Klassifikationsziel darstellt, bieten Surrogat-Verluste wie Hinge-, Logistischer und Exponentieller Verlust rechentechnisch handhabbare Alternativen mit unterschiedlichen Eigenschaften. Die Kreuzentropie (Logistisch und Kategorisch) ist der Standard für probabilistische Modelle, während der Hinge-Verlust mit dem Maximum-Margin-Prinzip von SVMs verbunden ist. Tabelle 2 fasst die Schlüsseleigenschaften und Formeln der besprochenen Verlustfunktionen zusammen. Beachten Sie, dass für die Logistische und Kategorische Kreuzentropie die Formeln mit Wahrscheinlichkeiten () oft direkter in Implementierungen verwendet werden, die Sigmoid- oder Softmax-Aktivierungen beinhalten. Die Formeln mit dem Score sind nützlich für den Vergleich mit dem Hinge- und Exponentiellen Verlust.
Tabelle 2: Vergleich von Klassifikations-Verlustfunktionen
| Verlustfunktion | Formel (Gängige Form) | Konvex? | Differenzierbar? | Empfindlichkeit ggü. Ausreissern | Use Cases |
|---|---|---|---|---|---|
| Null-Eins | () | Nein | Nein (f.ü.) | Gering | Evaluationsmetrik |
| Hinge | () | Ja | Nein (bei ) | Mittel | SVMs |
| Logistisch (BCE) | () ODER () | Ja | Ja | Mittel-Hoch | Logistische Regression, Neuronale Netze (Binär) |
| Kategorische Kreuzentropie | ( one-hot, W’keitsvektor, =wahre Klasse) | Ja | Ja | Mittel-Hoch | Neuronale Netze (Multiklasse) |
| Quadrat. Hinge | () | Ja | Ja | Hoch | L2-SVMs, Alternative zu Hinge |
| Exponentiell | () | Ja | Ja | Sehr Hoch | AdaBoost |
Hinweis: repräsentiert typischerweise den Rohwert (Score) oder Logit des Modells. und repräsentieren vorhergesagte Wahrscheinlichkeiten. Differenzierbarkeit bezieht sich auf stetige Differenzierbarkeit. f.ü. = fast überall.
4. Kontrastive Verlustfunktionen (Contrastive Losses)
Kontrastive Verlustfunktionen sind eine zentrale Komponente des kontrastiven Lernens, einer Methodik, die darauf abzielt, nützliche Repräsentationen von Daten zu lernen, oft ohne explizite Labels (im Rahmen des selbst-überwachten Lernens, Self-Supervised Learning, SSL) oder zur Verbesserung überwachter Modelle (Metric Learning). Die Grundidee besteht darin, eine Einbettungsfunktion (Encoder) zu trainieren, die Datenpunkte in einen niedrigdimensionalen Repräsentationsraum (Embedding Space) abbildet (), sodass ähnliche Datenpunkte nahe beieinander und unähnliche Datenpunkte weit voneinander entfernt liegen. Dies wird erreicht, indem man für einen gegebenen Ankerpunkt (anchor) :
- Positive Beispiele (z.B. andere Transformationen/Augmentationen desselben Datenpunkts, Punkte derselben Klasse) im Repräsentationsraum näher an den Anker heranzieht.
- Negative Beispiele (z.B. Datenpunkte aus anderen Bildern/Klassen) vom Anker wegstösst.
Der “Kontrast” entsteht durch den Vergleich der Ähnlichkeit zwischen dem Anker und positiven Beispielen gegenüber der Ähnlichkeit zwischen dem Anker und negativen Beispielen. Die Formulierung des Verlusts hängt entscheidend vom gewählten Ähnlichkeitsmass (Similarity Measure) und der spezifischen Struktur der positiven/negativen Paare oder Tripletts ab. Kontrastives Lernen findet breite Anwendung im selbst-überwachten Lernen für Computer Vision und NLP, im Metric Learning, in Empfehlungssystemen und bei der Gesichtserkennung.
4.1. Ähnlichkeitsmasse (Similarity Measures)
Die Wahl des Ähnlichkeitsmasses ist entscheidend dafür, wie “Nähe” und “Ferne” im Einbettungsraum quantifiziert werden. Die gängigsten Masse sind:
- Kosinus-Ähnlichkeit (Cosine Similarity): Misst den Kosinus des Winkels zwischen zwei Vektoren und . Sie ist unempfindlich gegenüber der Magnitude der Vektoren und konzentriert sich auf die Orientierung. Werte liegen im Bereich , wobei 1 perfekte Übereinstimmung, -1 entgegengesetzte Richtung und 0 Orthogonalität bedeutet. Oft verwendet für hochdimensionale Daten (wie Text-Embeddings oder Bild-Features) und typischerweise in Verbindung mit normalisierten Embeddings ().
- Euklidischer Abstand (-Distanz): Misst den geradlinigen Abstand zwischen zwei Punkten im Raum. Werte liegen im Bereich . Im Gegensatz zur Kosinus-Ähnlichkeit ist er empfindlich gegenüber der Magnitude. Kontrastive Verluste, die auf Distanz basieren, zielen darauf ab, die Distanz für positive Paare zu minimieren und für negative Paare zu maximieren (oft über eine Marge hinaus). Um ihn als Ähnlichkeitsmass zu interpretieren, kann eine invertierende Transformation verwendet werden (z.B. ).
- Skalarprodukt (Dot Product): Das einfache Skalarprodukt kann ebenfalls als Ähnlichkeitsmass dienen. Es ist jedoch stark von den Vektormagnituden abhängig. Wenn die Vektoren auf eine Einheitskugel normiert sind (), ist das Skalarprodukt äquivalent zur Kosinus-Ähnlichkeit.
Die Wahl des Masses beeinflusst die Geometrie des erlernten Repräsentationsraums und die Formulierung der Verlustfunktion.
Übersicht der Ähnlichkeits-/Distanzmasse:
| Mass | Formel | Wertebereich | Typische Verwendung (Kontrastives Lernen) |
|---|---|---|---|
| Kosinus-Ähnlichkeit | InfoNCE/NT-Xent, SSL, hohe Dimensionen | ||
| Euklidischer Abstand () | Contrastive Loss (Paar), Triplet Loss, Metric Learning | ||
| Skalarprodukt | Ähnlich zu Kosinus bei normierten Vektoren |
4.2. Contrastive Loss (Paar-basiert)
Dies ist eine der frühesten Formulierungen kontrastiven Lernens, oft verwendet in Siamesischen Netzwerken (Hadsell et al., 2006). Der Verlust wird separat für positive und negative Paare definiert.
Erklärung: Für ein Paar von Eingaben und deren Embeddings wird ein Label verwendet ( für ein positives Paar, für ein negatives Paar). Das Ziel ist, die Distanz für positive Paare klein zu halten und für negative Paare sicherzustellen, dass sie grösser als eine definierte Marge ist. Typischerweise wird der Euklidische Abstand verwendet.
Formel: Der Verlust für einen Datensatz von Paaren ist:
Hier ist die Distanz des -ten Paares, das Label des Paares, und die Marge. (Manchmal wird statt verwendet).
Motivation: Die Formel ist intuitiv:
- Wenn (positives Paar), ist der Verlust . Die Minimierung dieses Terms zieht positive Paare zusammen.
- Wenn (negatives Paar), ist der Verlust . Dieser Term ist nur dann grösser als null, wenn die Distanz kleiner als die Marge ist. Die Minimierung bestraft also negative Paare, die zu nah beieinander liegen, und drängt sie auseinander, bis ihre Distanz mindestens beträgt.
Eigenschaften und Herausforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Grundidee | Minimiere Distanz für positive Paare, maximiere sie über eine Marge für negative Paare. |
| Typisches Ähnlichkeitsmass | Euklidischer Abstand (). |
| Formel (pro Paar) | . |
| Vorteile |
|
| Nachteile/ Herausforderungen |
|
| Use Cases | Metric Learning, Gesichtserkennung/-verifikation, Signaturverifikation, Training Siamesischer Netzwerke. |
4.3. Triplet Loss
Der Triplet Loss (Weinberger et al., 2006; Schroff et al., 2015 - FaceNet) verwendet statt Paaren sogenannte Tripletts, bestehend aus einem Anker-, einem positiven und einem negativen Beispiel.
Erklärung: Für jedes Triplett mit Embeddings soll der Abstand zwischen Anker und Positivem kleiner sein als der Abstand zwischen Anker und Negativem , und zwar um eine Marge .
Formel: Der Verlust über Tripletts ist:
Auch hier wird oft der Euklidische Abstand verwendet, und manchmal werden die Distanzen nicht quadriert. ist die Marge.
Motivation: Der Verlustterm ist nur dann positiv, wenn . Die Minimierung des Verlusts erzwingt also . Dies stellt sicher, dass der Anker dem positiven Beispiel signifikant näher ist als dem negativen Beispiel.
Triplet Mining: Eine grosse Herausforderung ist die Auswahl von informativen Tripletts. Zufällige Tripletts führen oft zu einem Verlust von null (wenn die Bedingung bereits erfüllt ist) und somit zu langsamer Konvergenz. Strategien wie “Hard Negative Mining” (Auswahl von negativen Beispielen, die der Marge am nächsten kommen oder sie verletzen) sind entscheidend für den Erfolg.
Eigenschaften und Herausforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Grundidee | Erzwinge, dass der Anker dem positiven Beispiel um eine Marge näher ist als dem negativen Beispiel. |
| Typisches Ähnlichkeitsmass | Euklidischer Abstand (). |
| Formel (pro Triplett) | . |
| Vorteile |
|
| Nachteile/ Herausforderungen |
|
| Use Cases | Gesichtserkennung, Person Re-Identification, Bildsuche, Metric Learning im Allgemeinen. |
4.4. InfoNCE / NT-Xent Loss
InfoNCE (Information Noise Contrastive Estimation) ist ein moderner kontrastiver Verlust, der insbesondere im selbst-überwachten Lernen (SSL) sehr erfolgreich ist (z.B. in CPC, SimCLR, MoCo). NT-Xent (Normalized Temperature-scaled Cross Entropy) ist eine spezifische Implementierung davon, die in SimCLR verwendet wird.
Erklärung: Die Kernidee ist, das kontrastive Lernen als ein Klassifikationsproblem zu formulieren: Für einen Anker soll sein positives Beispiel aus einer Menge von negativen Beispielen korrekt identifiziert werden. Dies basiert auf der Maximierung der unteren Schranke der gegenseitigen Information (Mutual Information) zwischen verschiedenen “Sichten” (z.B. Augmentationen) desselben Datenpunkts. Typischerweise werden Kosinus-Ähnlichkeit und ein Temperatur-Skalierungsfaktor verwendet.
Formel (InfoNCE): Für einen Anker , sein positives Beispiel und negative Beispiele :
Dies hat die Form einer Softmax-Kreuzentropie, wobei die Logits durch die skalierten Ähnlichkeiten gegeben sind. ist typischerweise die Kosinus-Ähnlichkeit.
Formel (NT-Xent - SimCLR Variante): In SimCLR werden für jedes Bild in einem Batch der Grösse zwei augmentierte Versionen erzeugt, was zu Embeddings führt. Für ein positives Paar (die von demselben Originalbild stammen) werden alle anderen Embeddings im Batch als negative Beispiele betrachtet. Der Verlust für das Paar ist:
Der Gesamtverlust ist der Durchschnitt von über alle positiven Paare im Batch.
Temperatur : Der Temperaturparameter (typischerweise ein kleiner Wert wie 0.1 oder 0.07) skaliert die Ähnlichkeiten vor der Softmax-Funktion. Eine niedrige Temperatur erhöht die Konzentration der Verteilung und gewichtet “harte” negative Beispiele (solche, die dem Anker ähnlich sind) stärker.
Eigenschaften und Herausforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Grundidee | Identifiziere das positive Beispiel unter vielen negativen Beispielen (Klassifikations-Analogie). Maximiert Mutual Information. |
| Typisches Ähnlichkeitsmass | Kosinus-Ähnlichkeit. |
| Formel (InfoNCE) | Softmax-Kreuzentropie über skalierte Ähnlichkeiten. Siehe Gl. \eqref{eq:infonce_loss}. |
| Wichtige Aspekte |
|
| Vorteile |
|
| Nachteile/ Herausforderungen |
|
| Use Cases | Selbst-überwachtes Vorlernen von visuellen und sprachlichen Repräsentationen (SimCLR, MoCo, CPC, etc.). |
4.5. Vergleich Kontrastiver Verlustfunktionen
Kontrastive Verlustfunktionen bieten flexible Werkzeuge zum Lernen von Repräsentationen durch Vergleich. Die Wahl der Funktion hängt von der Aufgabe und den verfügbaren Daten ab. Die paar-basierte Contrastive Loss und die Triplet Loss sind oft im Metric Learning und bei Verifikationsaufgaben zu finden, wo explizite positive/negative Beziehungen (oft durch Labels) definiert sind oder leicht abgeleitet werden können; sie erfordern jedoch sorgfältiges Sampling oder Mining. InfoNCE/NT-Xent dominiert im modernen selbst-überwachten Lernen, wo positive Paare durch Datenaugmentation erzeugt werden und eine grosse Menge an negativen Beispielen (oft der Rest des Batches) verwendet wird, um robuste, allgemeine Repräsentationen zu lernen. Die Wahl des Ähnlichkeitsmasses ist ebenfalls entscheidend, wobei Kosinus-Ähnlichkeit bei InfoNCE und Euklidischer Abstand bei den älteren Methoden vorherrschen. Tabelle 3 fasst die Hauptunterschiede zusammen.
Tabelle 3: Vergleich von Kontrastiven Verlustfunktionen
| Verlustfunktion | Grundidee | Ähnlichkeitsmass (typ.) | Benötigt | Hauptvorteil | Hauptherausforderung |
|---|---|---|---|---|---|
| Contrastive Loss (Paar) | Nähe für Pos., Ferne () für Neg. | Eukl. Distanz () | Positive/Negative Paare, Marge | Intuitiv, gut für Verifikation | Sampling von Paaren, Marge |
| Triplet Loss | Anker näher an Pos. als an Neg. (mit Marge ) | Eukl. Distanz () | Tripletts (a, p, n), Marge | Lernt relative Ähnlichkeit | Triplet Mining, Marge |
| InfoNCE / NT-Xent | Identifiziere Pos. unter vielen Neg. (Klassifikation) | Kosinus-Ähnlichkeit | Pos. Paar, viele Negative, Temperatur | State-of-the-Art SSL, skaliert gut | Grosse Batches/Memory Bank, -Wahl |
Hinweis: SSL = Self-Supervised Learning. = Marge, = Temperatur.
5. Adversariale Verlustfunktionen (Adversarial Losses)
Adversariale Verlustfunktionen sind das Herzstück von Generative Adversarial Networks (GANs), einem populären Ansatz im Bereich der generativen Modellierung. GANs bestehen typischerweise aus zwei Komponenten, die in einem Minimax-Spiel gegeneinander antreten:
- Generator (G): Versucht, Daten zu erzeugen (z.B. Bilder, Texte), die von echten Daten nicht zu unterscheiden sind. Er nimmt einen Zufallsvektor aus einem Prior-Raum (z.B. einer Normalverteilung ) als Eingabe und erzeugt eine synthetische Probe . Das Ziel ist es, die Verteilung der generierten Daten so zu formen, dass sie der Verteilung der echten Daten möglichst ähnlich ist.
- Diskriminator (D): Versucht zu entscheiden, ob eine gegebene Datenprobe echt (aus ) oder künstlich (aus , also von G erzeugt) ist. Er gibt typischerweise einen Wert aus, der die Wahrscheinlichkeit (oder einen Score) repräsentiert, dass die Eingabe echt ist.
Der “adversariale Verlust” ergibt sich aus diesem kompetitiven Prozess. Der Diskriminator wird trainiert, um echte und künstliche Proben korrekt zu klassifizieren, während der Generator trainiert wird, um Proben zu erzeugen, die den Diskriminator täuschen. Dieses dynamische Gleichgewicht führt im Idealfall dazu, dass der Generator lernt, realistische Daten zu erzeugen. Verschiedene Formulierungen des adversarialen Verlusts wurden vorgeschlagen, um unterschiedliche Distanzmasse zwischen und zu optimieren oder um häufig auftretende Trainingsprobleme wie Modenkollaps (Mode Collapse) oder verschwindende Gradienten (Vanishing Gradients) zu mildern. Wir verwenden die folgende Notation: ist eine echte Datenprobe, ist ein Rauschvektor, ist eine generierte (künstliche) Probe, ist die Ausgabe des Diskriminators für eine echte Probe, und ist die Ausgabe des Diskriminators für eine künstliche Probe. bezeichnet den Erwartungswert über die echte Datenverteilung und den Erwartungswert über die Prior-Verteilung des Rauschens.
5.1. Minimax-Verlust (Original GAN)
Der ursprüngliche GAN-Verlust, vorgeschlagen von Goodfellow et al. (2014), basiert auf einem Minimax-Spiel, das theoretisch die Jensen-Shannon-Divergenz (JSD) zwischen der echten Datenverteilung und der Generatorverteilung minimiert.
Formel (Minimax-Ziel): Das Ziel ist es, das folgende Minimax-Problem zu lösen:
Hier wird angenommen, dass die Wahrscheinlichkeit ausgibt, dass die Eingabe echt ist (, typischerweise über eine Sigmoid-Aktivierung).
Herleitung/Motivation: Die Zielfunktion entspricht der binären Kreuzentropie für einen Klassifikator , der echte Daten (Label 1) von künstlichen Daten (Label 0) unterscheiden soll. Bei optimalem Diskriminator reduziert sich das Minimax-Problem zu . Die Minimierung bezüglich minimiert also die JSD zwischen der echten und der generierten Verteilung.
Separate Verluste für das Training: In der Praxis werden G und D abwechselnd trainiert, wobei separate Verlustfunktionen minimiert werden:
- Diskriminator-Training: Maximiere bezüglich . Dies ist äquivalent zur Minimierung des negativen , was einer Standard-Kreuzentropie-Verlustfunktion entspricht:
- Generator-Training (Original): Minimiere bezüglich . Dies entspricht der Minimierung von . Dieses Ziel leidet jedoch unter dem Problem der saturierenden Gradienten: Wenn der Diskriminator die künstlichen Proben sehr gut erkennt (), wird der Gradient von bezüglich der Parameter von G sehr klein, was das Lernen verlangsamt oder stoppt.
- Generator-Training (Non-Saturating Heuristik): Um das Sättigungsproblem zu umgehen, wird in der Praxis oft ein alternatives Ziel für G verwendet: Maximiere , was äquivalent zur Minimierung von
ist. Dieses Ziel liefert stärkere Gradienten, besonders zu Beginn des Trainings.
Eigenschaften und Herausforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Ziel (theoretisch) | Minimierung der Jensen-Shannon-Divergenz (JSD) zwischen und . |
| Diskriminator-Verlust | Standard Binäre Kreuzentropie (BCE). Siehe Gl. \eqref{eq:gan_loss_d}. |
| Generator-Verlust (non-saturating) | Modifizierte BCE, um Gradientensättigung zu vermeiden. Siehe Gl. \eqref{eq:gan_loss_g_ns}. |
| Vorteile |
|
| Probleme/ Herausforderungen |
|
| Use Cases | Grundlage für viele frühe GAN-Architekturen. Wird oft als Basis oder zum Vergleich herangezogen. |
5.2. Wasserstein-Verlust (WGAN & WGAN-GP)
Der Wasserstein-GAN (WGAN)-Verlust, vorgeschlagen von Arjovsky et al. (2017), zielt darauf ab, die Trainingsstabilität von GANs zu verbessern, indem statt der JSD die Wasserstein-1-Distanz (auch Earth Mover’s Distance, EMD) minimiert wird. Die W-Distanz hat auch bei disjunkten Verteilungen aussagekräftigere Gradienten.
Formel (Wasserstein-1-Distanz): Die W-1-Distanz zwischen und ist definiert als:
wobei das Supremum über alle 1-Lipschitz-Funktionen genommen wird. Im WGAN-Kontext wird die Funktion durch den Kritiker (Critic, ) approximiert, der an die Stelle des Diskriminators tritt. Der Kritiker gibt einen unbeschränkten Score aus, keine Wahrscheinlichkeit.
Verlustfunktionen:
- Kritiker-Training: Der Kritiker wird trainiert, um den Ausdruck in Gl. \eqref{eq:wasserstein1} zu maximieren. Dies entspricht der Minimierung von:
- Generator-Training: Der Generator wird trainiert, um die W-Distanz zu minimieren. Da nicht von abhängt, entspricht dies der Maximierung von , oder der Minimierung von:
Durchsetzung der Lipschitz-Bedingung: Die grösste Herausforderung bei WGANs ist die Sicherstellung, dass der Kritiker (approximativ) 1-Lipschitz bleibt.
- WGAN (Weight Clipping): Die ursprüngliche Methode beschränkt die Gewichte des Kritikers auf einen kleinen Bereich (z.B. ). Dies ist einfach, kann aber zu Optimierungsproblemen oder reduzierter Kapazität des Kritikers führen.
- WGAN-GP (Gradient Penalty): Gulrajani et al. (2017) schlugen vor, der Kritiker-Verlustfunktion einen Strafterm hinzuzufügen, der Abweichungen des Gradientennormen von 1 bestraft:
Hierbei ist eine Stichprobe, die zufällig zwischen einer echten Probe und einer künstlichen Probe interpoliert wird ( ist die Verteilung dieser interpolierten Punkte), und ist ein Hyperparameter (oft ). . Diese Methode ist stabiler und führt oft zu besseren Ergebnissen.
Eigenschaften und Anforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Ziel (theoretisch) | Minimierung der Wasserstein-1-Distanz zwischen und . |
| Kritiker-Verlust (WGAN-GP) | . |
| Generator-Verlust | . |
| Vorteile |
|
| Nachteile/ Anforderungen |
|
| Use Cases | Sehr populär für Bildgenerierung und andere generative Aufgaben, bei denen Stabilität wichtig ist. Basis für viele fortgeschrittene GANs. |
5.3. Least Squares Verlust (LSGAN)
Der Least Squares GAN (LSGAN), vorgeschlagen von Mao et al. (2017), ersetzt die Sigmoid-Kreuzentropie-Verluste des originalen GAN durch Least-Squares-(Quadratmittel)-Verluste.
Formel: Der Diskriminator (der hier wieder unbeschränkte Scores ausgibt) und der Generator minimieren folgende Verlustfunktionen, wobei Zielwerte sind:
Eine übliche Wahl der Parameter ist (oder alternativ ). Mit versucht der Diskriminator, echte Proben auf 1 und künstliche auf 0 zu mappen. Mit versucht der Generator, den Diskriminator dazu zu bringen, seine künstlichen Proben als 1 zu klassifizieren.
Motivation: Die Verwendung des quadratischen Fehlers bestraft Proben, die zwar auf der korrekten Seite der Entscheidungsgrenze liegen, aber weit davon entfernt sind. Dies kann zu stabileren Gradienten führen als die Sigmoid-Kreuzentropie, die für “zu einfach” klassifizierte Proben sättigt (Gradient wird klein). LSGAN zielt darauf ab, die künstlichen Daten näher an die Entscheidungsgrenze zu “ziehen”, die durch die echten Daten definiert ist.
Eigenschaften und Herausforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Ziel | Minimierung eines Pearson -Divergenz-ähnlichen Ziels (implizit). Stabilisierung des Trainings durch Vermeidung von Gradientensättigung. |
| Diskriminator-Verlust | Quadratischer Fehler zu Zielwerten (fake) und (real). Siehe Gl. \eqref{eq:lsgan_loss_d}. |
| Generator-Verlust | Quadratischer Fehler zum Zielwert (oft derselbe wie ). Siehe Gl. \eqref{eq:lsgan_loss_g}. |
| Vorteile |
|
| Probleme/ Herausforderungen |
|
| Use Cases | Weit verbreitete Alternative zum originalen GAN-Verlust, besonders bei Bildgenerierungsaufgaben. |
5.4. Hinge-Verlust (Adversarial Hinge Loss)
Eine weitere populäre Alternative, die oft in modernen GANs wie SAGAN oder BigGAN verwendet wird, ist die Adaption des Hinge-Verlusts für das adversariale Training.
Formel (Gängige Variante): Der Diskriminator (der unbeschränkte Scores ausgibt) und der Generator minimieren folgende Hinge-basierte Verluste:
Hierbei versucht der Diskriminator, echte Proben auf einen Score von und künstliche Proben auf einen Score von zu bringen. Der Generator versucht, die Scores seiner künstlichen Proben zu maximieren (also zu minimieren).
Motivation: Ähnlich wie der Standard-Hinge-Verlust in der Klassifikation, zielt diese Formulierung auf eine maximale Marge zwischen den Scores für echte und künstliche Daten ab. Sie bestraft nur Scores, die die Marge verletzen. Dies hat sich empirisch als sehr effektiv für stabiles Training und hohe Ergebnisqualität erwiesen.
Eigenschaften und Herausforderungen:
| Eigenschaft | Beschreibung |
|---|---|
| Ziel | Maximierung der Marge zwischen den Scores für echte und künstliche Daten. |
| Diskriminator-Verlust | Summe zweier Hinge-Terme für echte () und künstliche () Samples. Siehe Gl. \eqref{eq:hingegan_loss_d}. |
| Generator-Verlust | Maximierung des Diskriminator-Scores für künstliche Samples. Siehe Gl. \eqref{eq:hingegan_loss_g}. |
| Vorteile |
|
| Probleme/ Herausforderungen |
|
| Use Cases | Standardwahl in vielen modernen, hochleistungsfähigen GAN-Architekturen (z.B. SAGAN, BigGAN) für Bildsynthese. |
5.5. Vergleich Adversarialer Verlustfunktionen
Die Wahl der adversarialen Verlustfunktion hat erheblichen Einfluss auf die Stabilität des Trainingsprozesses und die Qualität der generierten Ergebnisse. Während der originale Minimax-Verlust eine klare theoretische Grundlage hat (JSD-Minimierung), leidet er oft unter praktischen Problemen. WGANs bieten eine verbesserte theoretische Fundierung (Wasserstein-Distanz) und empirische Stabilität, erfordern aber die Handhabung der Lipschitz-Bedingung. LSGAN und der adversariale Hinge-Verlust sind pragmatische Alternativen, die oft gute Stabilität und Leistung durch Modifikation der Zielfunktion erreichen, um Gradientenprobleme zu vermeiden. Die Wahl hängt oft von der spezifischen Anwendung, der Architektur und den verfügbaren Rechenressourcen ab. Tabelle 4 bietet einen zusammenfassenden Überblick.
Tabelle 4: Vergleich von Adversarialen Verlustfunktionen
| Verlustfunktion | Ziel (Distanz/Div.) | D-Output | G-Verlust (typisch, min.) | Hauptvorteil | Hauptherausforderung |
|---|---|---|---|---|---|
| Original GAN (Minimax) | JSD (theor.) | W’keit | Theor. Fundierung | Instabilität, Vanishing Gradients | |
| WGAN-GP | Wasserstein-1 | Score | Stabilität, Korrelation mit Qualität | Lipschitz (Gradient Penalty) | |
| LSGAN | Pearson -ähnlich | Score | Stabilität ggü. Original-GAN | Weniger theor. fundiert als WGAN | |
| Adversarial Hinge | Margin Maximierung | Score | Empirisch hohe Leistung & Stabilität | Weniger klare Divergenz-Interpretation |
Hinweis: JSD = Jensen-Shannon Divergence. D = Diskriminator, C = Kritiker, G = Generator. G-Verluste sind zur Minimierung dargestellt.
References
[1] I. Goodfellow et al., “Generative Adversarial Nets,” in Advances in Neural Information Processing Systems 27 (NIPS 2014), 2014, pp. 2672–2680.
[2] R. Hadsell, S. Chopra, and Y. LeCun, “Dimensionality Reduction by Learning an Invariant Mapping,” in 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), 2006, vol. 2, pp. 1735–1742.
[3] K. Q. Weinberger and L. K. Saul, “Distance Metric Learning for Large Margin Nearest Neighbor Classification,” Journal of Machine Learning Research, vol. 10, pp. 207-244, 2009.
[4] F. Schroff, D. Kalenichenko, and J. Philbin, “FaceNet: A Unified Embedding for Face Recognition and Clustering,” in 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015, pp. 815–823.
[5] M. Arjovsky, S. Chintala, and L. Bottou, “Wasserstein GAN,” in Proceedings of the 34th International Conference on Machine Learning (ICML 2017), 2017, pp. 214–223.
[6] I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin, and A. C. Courville, “Improved Training of Wasserstein GANs,” in Advances in Neural Information Processing Systems 30 (NIPS 2017), 2017, pp. 5767–5777.
[7] X. Mao, Q. Li, H. Xie, R. Y. K. Lau, Z. Wang, and S. Paul Smolley, “Least Squares Generative Adversarial Networks,” in 2017 IEEE International Conference on Computer Vision (ICCV), 2017, pp. 2794–2802.