
Review Zurich NLP #17
Review ZurichNLP #17
Author: Philipp Gérard Trémuel
About the Event
Aleksander Ficek (NVIDIA): Synthetic Generators and Verifiers for Coding TBD
Matteo Saponati (ETH Zurich): Structure of Self-Attention Beyond Queries and Keys
Self-attention is essential to Transformer architectures, yet how information is embedded in the self-attention matrices and how different objective functions impact this process remains unclear. We present a mathematical framework to analyze self-attention matrices by deriving the structures governing their weight updates. Using this framework, we demonstrate that bidirectional training induces symmetry in the weight matrices, while autoregressive training results in directionality and column dominance. Our theoretical findings are validated across multiple Transformer models - including ModernBERT, GPT, LLaMA3, and Mistral - and input modalities like text, vision, and audio. Finally, we apply these insights by showing that symmetric initialization improves the performance of encoder-only models on language tasks. This mathematical analysis offers a novel theoretical perspective on how information is embedded through self-attention, thereby improving the interpretability of Transformer…
🧠 Synthetic Data for Code and Reasoning in LLMs
Aleksander Ficek (NVIDIA)
🚀 The Rise of Reasoning Models
The field of LLMs entered a reasoning-driven renaissance at the end of 2024, ignited by OpenAI’s O1 in December 2024 and followed by DeepSeek-R1 in January 2025. These models showcased the next step of beyond chain-of-thought (CoT) reasoning and how breaking down complex problems step by step could be embedded into training, not just inference by using Reinforcement Learning (RL).
Yet, contrary to earlier belief that RL was essential for state-of-the-art reasoning, OpenCodeReasoning has shown that supervised fine-tuning (SFT) alone—on a large synthetic dataset—can achieve comparable results on coding benchmark.
⚙️ OpenCodeReasoning: SFT-Only Reasoning Mastery
- Dataset Scale & Method
- Over 736K Python code solutions with full reasoning traces, covering 28,900+ unique competitive programming tasks.
- Solutions are generated by a strong teacher model (like DeepSeek‑R1), then validated via unit tests and distilled into student models.
- Performance Highlights
- Qwen2.5 fined-tuned with this dataset hits pass@1 rates of 51.3% (7B), 59.4% (14B), and 61.8% (32B) on LiveCodeBench—beating comparable SFT-only baselines and matching DeepSeek‑R1-distilled versions.
- Surpasses reinforcement‑learning-enhanced models on code tasks, validating pure SFT scaling.
- Insights
- Scaling SFT data yields steady performance gains—no evidence of plateauing.
- Surprisingly, including some incorrect solutions alongside unit-tests in the dataset boosts model robustness on hard problems.
- Limitations
- Pure SFT lacks internal self-correction: models often stick to their own faulty answers .
- Improving via SFT-only might hit a ceiling—hence NVIDIA’s next step.
🎯 NVIDIA’s Llama-Nemotron: SFT + RL = Efficiency & Power
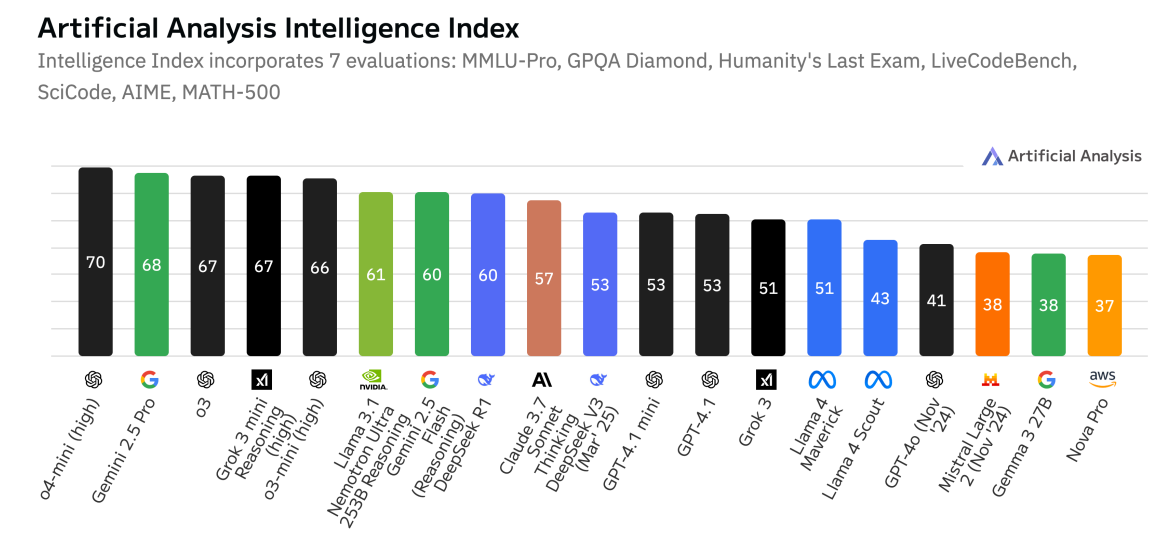 Figure 1 | As of April 2025, our flagship model LN-Ultra is the most “intelligent” open model according to Artificial Analysis.
Figure 1 | As of April 2025, our flagship model LN-Ultra is the most “intelligent” open model according to Artificial Analysis.
-
Llama‑Nemotron (Nano 8B, Super 49B, Ultra 253B) [Paper]
Try Llama-3_1-nemotron-70b-instruct
- Heterogeneous models optimized via Neural Architecture Search (NAS) for faster inference and better memory use.
- Support a dynamic “reasoning toggle”—users can switch detailed reasoning on/off in real time.
- Trained in stages:
- Architecture optimization + distillation + continued pretraining
- Supervised fine-tuning on reasoning tasks (including traces from DeepSeek-R1)
- Large-scale reinforcement learning on STEM datasets
- Short human-alignment tuning.
-
Performance
- Ultra‑253B outperforms DeepSeek‑R1 on many reasoning benchmarks, while maintaining 4× higher throughput and fitting on a single 8‑GPU node.
- Hits 76% on GPQA-Diamond (PhD-level science reasoning!?), compared to 65% for humans.
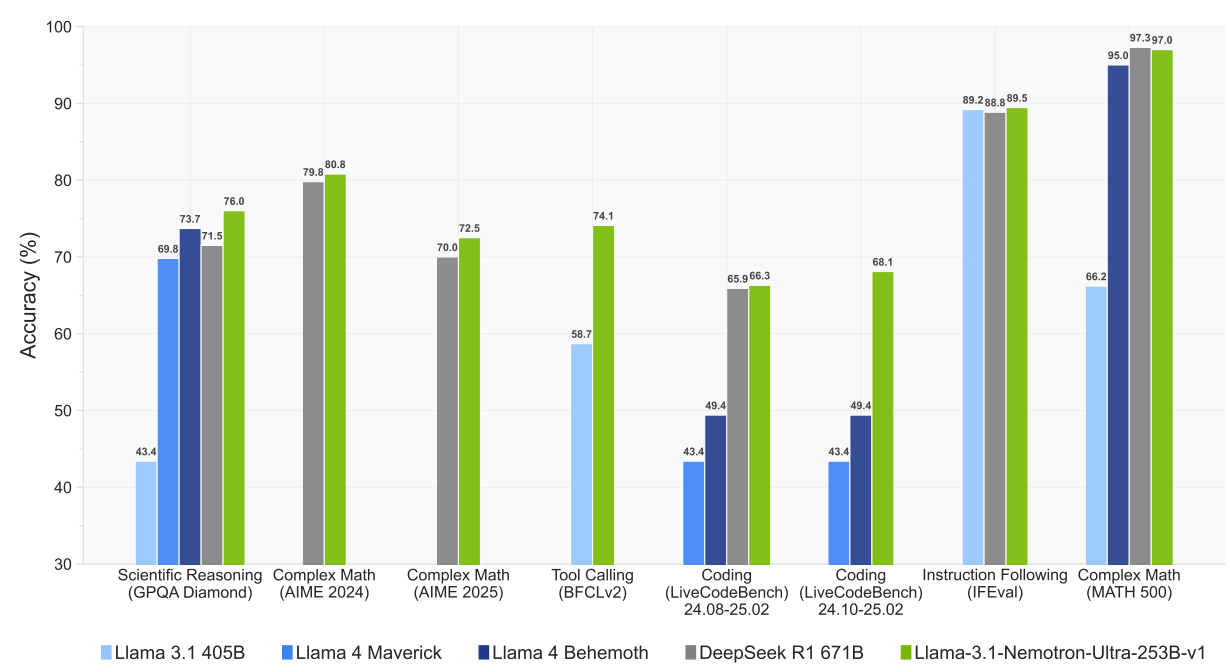 Figure 2 | LN-Ultra delivers leading performance among open models across a wide range of reasoning and non-reasoning benchmarks.
Figure 2 | LN-Ultra delivers leading performance among open models across a wide range of reasoning and non-reasoning benchmarks.
- Open & Production‑Ready
- All models, weights, datasets, and tools (NeMo, Megatron‑LM, NeMo‑Aligner) are open under NVIDIA’s permissive license.
- Available via NIM microservices and Hugging Face, integrated across cloud and enterprise AI platforms
🔍 SFT-only vs SFT+RL: Trade-offs & Challenges
| Aspect | SFT-Only (OpenCodeReasoning) | SFT+RL (Nemotron) |
|---|---|---|
| Performance (Code) | ≈61.8% pass@1 (32B) | Nemotron Super/Ultra matches or exceeds SFT-only |
| Reasoning Self‑check | Limited; often fails on self-reflection → observation from the NVIDIA researchers | RL enhances quality and internal error correction. As mentioned in the talk, this is reached by using an external LLM judge |
| Inference Efficiency | Depends on architecture | Optimized via NAS, offering 4–5× faster throughput |
| Training Complexity | Simpler, stable, reproducible (SFT) | Harder: RL, reward design, stability issues |
| Resource Requirements | Lower; one stage SFT | Multi-stage: SFT + large‑scale RL |
| Adaptability | Strong for coding; limited beyond | Excels in math, science, coding, tool-use |
🤔 Reflections: Where Do We Go from Here? (Personal Thoughs)
- Blending SFT with targeted RL (as done by Nemotron) yields powerful, efficient models with improved reasoning and error correction.
- The approach of using an LLM-Judge is similar to a game‑theoretical setup, like a consensus or competitive game. The stability and fairness between Generator (model) and Judge (RL objective) can be critical.
- How to ensure stable training and reach an equilibrium like in training GANs?
- How to ensure the Judge isn’t hallucinating?
- In my opinion, an external “evaluator” like a code execution engine or unit tests is still required. Maybe they use the Judge to define the unit tests.
🧭 In Conclusion
- OpenCodeReasoning has redefined how far pure SFT can go by scaling synthetic reasoning datasets that can rival RL-enhanced approaches in coding benchmarks.
- NVIDIA’s Llama-Nemotron, by integrating SFT with large-scale RL and architecturally efficient designs, raises the bar further, delivering fast, high-accuracy reasoning in real-world formats.
- The quest ahead? Developing models that aren’t just smart, but truly inventive and trustworthy, capable of generating novel, correct solutions.
🧠 The Underlying Structures of Self-Attention: Symmetry, Directionality & Emergent Dynamics
Matteo Saponati (ETH Zurich)
The paper “The underlying structures of self-attention: symmetry, directionality, and emergent dynamics in Transformer training” dives deep into the often-overlooked geometry of the Q–K weight products in self-attention, revealing how different training objectives sculpt their fundamental structure—and even how those structures can be harnessed to improve model performance.
🔍 What Problem Are They Tackling?
While self-attention was a breakthrough in Transformers by mapping queries and keys (via , ) into attention patterns via it’s still not well understood why it works so well. This paper builds a mathematical framework that connects gradient dynamics to specific structural patterns in the joint query-key matrix ( , also referred to as ) .
Figure 3 | Illustration of the computation of the self-attention score between token and token .
🧩 Symmetry vs. Directionality: The Core Insights
- Autoregressive (decoder-only) training
- Predicts each token from the past only.
- The resulting updates to are asymmetric and create column dominance, introducing a learned directionality in the matrix.
- Bidirectional (encoder-only) training
- Enables tokens to condition on both past and future context.
- This results in symmetric weight updates, leading to highly symmetric matrices.
These differences are not just theoretical—they’re measurable.
Figure 4 | a) Left) Median symmetry score of the matrix as a function of the total number of parameters.
Each dot corresponds to the median and the interquartile range across layers of a given pre-trained model (see
Tables in Appendix S5). Right) Example of structures in the matrix of an encoder-only model (BERT
Tiny, layer 1 [Turc et al., 2019]) b) Left) Same as in a for the median directionality score of the matrix Wqk.
Right) Example of structures in the Wqk matrix of a decoder-only model (TinyStories GPT, layer 1 [Eldan and Li, 2023])
📊 Experiments Confirm Theory
- The authors introduced symmetry and directionality scores to quantify structural biases in .
- Evaluated across multiple models (e.g., BERT, GPT, LLaMA3, Mistral) and even audio/vision modalities, they consistently found:
- Encoder-only models → high symmetry scores
- Decoder-only models → high directionality scores
They further tracked how these scores evolve during training—symmetry steadily grows in encoder models, while directionality becomes pronounced in decoder models .
⚙️ Practical Payoff: Symmetric Initialization
Inspired by the theory, they experiment with enforcing symmetry in initialization for encoder-only models. The result?
✅ Faster convergence and better final performance on language tasks—demonstrating a clear practical benefit.
📝 Correcting Common Misconceptions
On QK math: Yes, . and are separate projections; they don’t multiply as , but rather as , and then forms the bilinear attention.
- On directional models: Autoregressive models will show early-token bias, but the structural phenomena revealed are broader—they reflect the gradient dynamics, not just inference behavior.
- On impact scope: While the paper doesn’t propose a new LLM architecture, it illuminates the internal mechanisms of self-attention, offering interpretability and practical optimization opportunities.
🚀 Why This Matters
- Theoretically rich: Bridges Transformer updates with bilinear algebra.
- Empirically solid: Consistent across architectures and data modalities.
- Pragmatically useful: Simple symmetric init yields measurable gains.
- Interpretability boost: Helps us “peek under the hood” of self-attention dynamics.
📌 Takeaways for Researchers & Practitioners
- Be conscious: encoder-only vs decoder-only training induces different geometric biases in .
- Consider symmetric initialization in encoder settings—it may enhance convergence.
- Use the symmetry/directionality scores as tools to analyze internal structure during model diagnostics.
This paper offers a mathematically grounded, empirically validated lens into how training objectives shape self-attention dynamics—revealing symmetry in bidirectional models and directionality in autoregressive ones. The icing on the cake: initializing self-attention weight matrices symmetrically actually helps. Not revolutionary, but a meaningful step forward in understanding and improving Transformers 🔧.