
NNUE: A Deep Dive into Modern Chess Engines
NNUE: A Deep Dive into Modern Chess Engines
Author: Roger Näf, MSE Student, Institute for Computational Engineering ICE, OST
This blog post takes a closer look at how modern chess engines use neural networks to think smarter and faster. It focuses on the Efficiently Updatable Neural Network (NNUE), a design that is perfectly suited to the specific challenges of chess. NNUE represents chess positions using a compact “HalfKP” encoding and updates them with a clever “Accumulator” system, allowing only the changed parts of a position to be recalculated. This makes evaluations lightning-fast, even on regular CPUs. The article also explains how NNUE works alongside powerful search algorithms to plan ahead and select moves that improve the overall game position, rather than just aiming for the best-looking immediate option. An approach that could inspire strategies in other games and real-time decision-making tasks.
1. Introduction: The Dawn of Superhuman Chess
Chess has been a fascinating game for centuries, challenging not only human intelligence but also serving as a testing ground for artificial intelligence. The historic moment when IBM’s Deep Blue defeated world champion Garry Kasparov in 1997 marked a pivotal shift [1]. It became clear that no human could surpass the capacity of a chess program. With several million calculated chess positions per second, Deep Blue defeated even the strongest chess players. Since chess programs reached a superhuman level, they have been continuously developed. A significant milestone in this development is the optimization of neural networks in chess engines, as realized with the NNUE architecture [2].
2. Chess: The Perfect AI Playground
Before diving into the neural network magic, let’s establish our foundation. Chess might seem like a simple game, but its complexity is staggering. Chess is a strategic board game for two players, played on an 8×8 grid consisting of alternating light and dark squares. Each player begins with 16 pieces: one king, one queen, two rooks, two bishops, two knights, and eight pawns. The goal of the game is to checkmate the opponent’s king, i.e., to place the king so that it can be immediately captured without there being a legal move to escape. White always begins the game, and the players then alternate turns [4].

Each type of piece moves in a specific way. The king can move one square in any direction, while the queen can move any number of squares in a straight line vertically, horizontally, or diagonally. Rooks move in straight lines along rows or columns, bishops move diagonally, and knights move in an L-shape (two squares in one direction and one in an orthogonal direction). Pawns move one square forward but capture diagonally. On the first move of a pawn, it has the option of moving two squares forward. When a pawn reaches the opposite end of the board, it is converted into another piece, usually a queen [4].
| Piece | Symbol | Count | Special Abilities |
|---|---|---|---|
| King | K | 1 | The VIP that must survive: one step in any direction |
| Queen | Q | 1 | The powerhouse: moves diagonally, horizontally, and vertically |
| Rook | R | 2 | The straight-line specialist: horizontal and vertical movement |
| Bishop | B | 2 | The diagonal dancer: moves diagonally |
| Knight | N | 2 | The tricky L-shaped jumper: L-shape (2+1 squares) |
| Pawn | P | 8 | The foot soldier: one step forward (two steps possible on first move), captures diagonally |
In chess, there are additional special rules to consider. Castling is a move involving the king and one of the rooks. It allows the king to move two squares towards the rook, and the rook moves to the square that the king has crossed. This move is only allowed if both pieces have not been moved before, the squares between them are empty, and the king is not in check. En passant is a special pawn capture that occurs when an opponent’s pawn moves two squares forward from its starting position and lands next to your own pawn. You can capture it in this move as if the opponent’s pawn had only moved one square [4].
A chess game can end in several ways. The most decisive is checkmate, in which one player successfully captures the opponent’s king. Other endings are stalemate, when a player has no legal moves but is not in check (leading to a draw), and a draw by agreement between the players. There are also technical draws such as threefold repetition (the same position is repeated three times), the 50-move rule (no capture or pawn move in fifty moves), and insufficient material, when neither player has enough material to checkmate the other [4].
3. NNUE: The Game-Changing Architecture
Now for the revolutionary part. NNUE isn’t just another neural network. It’s specifically designed for the unique demands of chess engines.
3.1 HalfKP: A New Way to See Chess
HalfKP (Half-King-Piece relationship) is a binary encoding of a chess position. The game position is viewed from the perspective of both players. Thereby, it encodes the relationship between each king and every piece on the board. For one player, the following triplets are evaluated [5]:
(own king, own piece, piece position)
(own king, opponent piece, piece position)This creates a representation of a chess position that consists mostly of zeros. To illustrate this, consider the starting position of a chess game. Only zeros are created until the king position e1 is reached for the first time [5]:
(own king a1, own queen a1) => 0
(own king a1, own queen b2) => 0
...
(own king e1, own queen c1) => 0
(own king e1, own queen d1) => 1
(own king e1, own queen e1) => 0
...All 64 king positions, 10 piece types (own/opponent queen, rook, bishop, knight, and pawn), and their 64 possible positions are considered. Thus, 40,960 (64×10×64) input bits per player are needed, totaling 81,920 (40,960×2) for a chess position. While this seems disadvantageous, this structure can be optimally updated, as described in the next section [5].
3.2 The “Efficiently Updatable” Magic: The Accumulator
Here’s where NNUE gets clever. In chess, only one piece moves at a time, so most of those 81,920 features stay the same between moves. Instead of recalculating everything from scratch, NNUE uses an accumulator that simply updates the few features that actually changed [5]. Thus, only a few bits change the input from zero to one or vice versa. This is exploited by the accumulator to update the position with minimal computational power. Individual pieces can be updated as follows [6]:
accumulator += weights[(A1, C3, pawn, white)];The weight calculation of a piece must be optimized. To treat this problem as focused as possible, only the calculation of the first layer of a player without biases is considered. Here, is the weight of input connected to node of the first layer, and is an input bit [5].
The calculation becomes:
Many of the are zero, so it’s much more sensible to calculate the desired values iteratively rather than multiplying the matrices (as would happen in a general neural network with GPU support) [5].
- First, initialize the result
- Then, for each in :
- If is zero, skip this element and continue with the next
- If is not zero, update the result
Thus, can be treated iteratively. Since is only non-zero in a few cases, only a short loop is executed. Being an input bit, can only be either zero or one, and therefore
This allows the vector to be calculated, which has one column and 255 rows. If a move is now made that is not a king move, there is only one input (for example, ) that changes from one to zero for the position where the piece was, and one input (for example, ) that changes from zero to one where the piece is placed. To obtain the new values , the accumulator must perform the following calculation [5].
This calculation is much more efficient than the initial matrix multiplication. To make NNUE even more efficient in chess engines, values are quantized and optimized for CPU operations. This makes NNUE incredibly fast. Fast enough to run efficiently on regular CPUs, as the operations are reduced to simple additions and subtractions [6].
3.3 The Complete Architecture: Two Perspectives, One Evaluation
NNUE’s architecture is elegantly simple yet powerful. The network takes both players’ perspectives as separate inputs, processes them through shared weights, then merges them for a final evaluation. The output is typically mapped to a centipawn scale where 0 represents a lost position, 0.5 represents equality, and 1.0 represents a winning advantage [6].
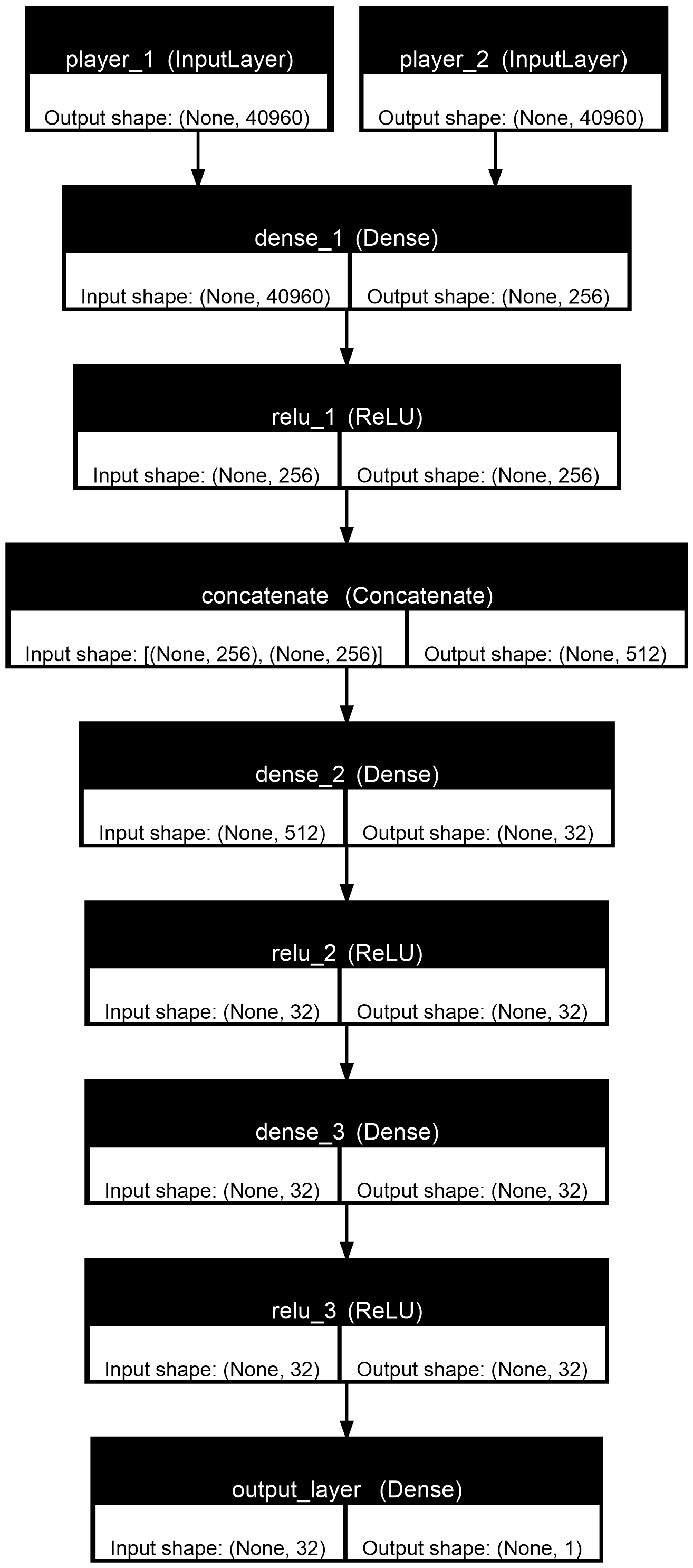
3.4 Planning Ahead: Search Algorithm
To predict the best move with the NNUE architecture, several moves in the future are analyzed. This does not result in the next best move being selected, but rather improves the overall chess position. These future chess positions are analyzed using a search algorithm. In chess, the MCTS (Monte Carlo Tree Search) and Alpha-Beta Search algorithms are the most widely used . MCTS is used to create a search tree, which is searched using a heuristic. Alpha-Beta Search creates a complete search tree, which is limited by its depth. If a chess engine can evaluate positions more efficiently, Alpha-Beta Search is usually preferred [5]:
| Chess Engine | Positions per Second | Search Algorithm |
|---|---|---|
| Deep Blue [1] | 200,000,000 | Alpha-Beta Search |
| Stockfish 8 [3] | 70,000,000 | Alpha-Beta Search |
| AlphaZero [7] | 80,000 | MCTS |
Alpha-Beta Search optimizes the search of the complete game tree. Alpha is the best score that the maximizing player can guarantee so far. Beta is the best score that the minimizing player can guarantee so far. If the search determines that a move leads to a worse result than a previously examined move, this branch is cut off, as the opponent will never allow this result [8].
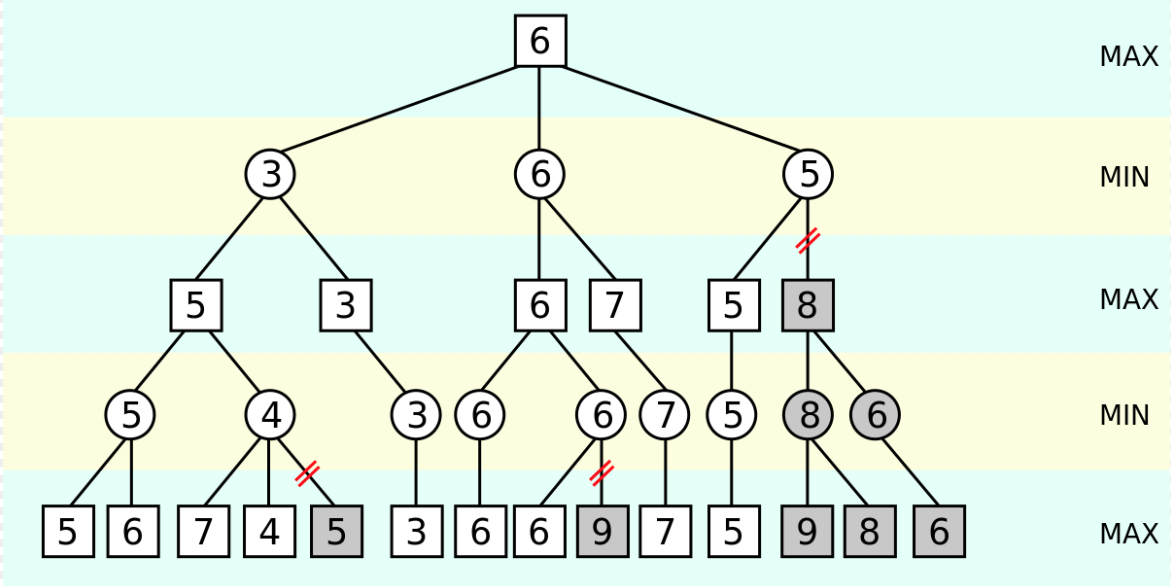
4. Conclusion and Outlook
The NNUE architecture represents a significant advancement in the field of game-playing artificial intelligence, demonstrating that carefully designed neural networks can achieve superhuman performance while maintaining computational efficiency suitable for real-time applications with minimal hardware requirements. NNUE’s primary theoretical contribution lies in its demonstration that domain-specific neural network architectures can substantially outperform both traditional hand-crafted evaluation functions and general-purpose deep learning approaches when applied to discrete, combinatorial domains. The HalfKP feature representation and accumulator-based update mechanism constitute novel contributions to efficient neural network inference in resource-constrained environments. The architecture’s success challenges conventional wisdom regarding the trade-offs between model complexity and inference speed, suggesting that carefully designed sparse representations can achieve superior performance characteristics compared to dense neural networks in specific problem domains. The successful deployment of NNUE in production chess engines suggests potential applications in related domains including other board games, real-time strategy optimization and other domains where rapid evaluation of incrementally changing states is required. Additionally, further research into the theoretical foundations of accumulator-based neural networks may yield insights applicable to broader classes of machine learning problems involving temporal or sequential data with sparse update patterns.
References
[1] Campbell, M.; Hoane, A.; Hsu, F.-h.: Deep Blue. Artificial Intelligence. 134 (Jan. 2002), pp. 57–83.
[2] Nasu, Y.: Efficiently Updatable Neural-Network-based Evaluation Functions for Computer Shogi. Apr. 28, 2018.
[3] Stockfish · GitHub. June 12. 2025. https://github.com/official-stockfish.
[4] Chess.com - Play Chess Online - Free Games. June 12. 2025. https://www.chess.com/
[5] Klein, D.: Neural Networks for Chess The magic of deep and reinforcement learning revealed. June 11, 2022.
[6] nnue-pytorch/docs/nnue.md at master · official-stockfish/nnue-pytorch · GitHub. June 12. 2025. https://github.com/official-stockfish/nnue-pytorch/blob/master/docs/nnue.md
[7] Silver, D.; Hubert, T.; Schrittwieser, J. et al.: Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm. Dec. 5, 2017.
[8] Crafter, O. t. P. t. B. a. S.: Alpha Beta Pruning In Minimax. On the Path to Becoming a Software Crafter. Jan. 2, 2018. https://www.ericdrosado.com/2018/01/02/alpha-beta-pruning-in-minimax.html