ICE Industrial-AI 🧠🤖
Gradient Boosting

Gradient Boosting


Latest

Gradient Boosting

Author: Christoph Würsch, ICE, Eastern Switzerland University of Applied Sciences, OST

Die Strategie des sequenziellen Lernens

Boosting ist ein mächtiges und weit verbreitetes Ensemble-Lernverfahren im Bereich des Machine Learning. Im Gegensatz zu Bagging-Methoden wie Random Forests, bei denen viele Modelle unabhängig voneinander trainiert und dann aggregiert werden, verfolgt Boosting einen sequenziellen Ansatz. Die Grundidee ist, die Vorhersagekraft vieler schwacher Lerner (sogenannte Weak Learners), die oft nur wenig besser sind als zufälliges Raten, schrittweise so zu bündeln, dass am Ende ein starker Ensemble-Lerner entsteht. Der Schlüssel zum Erfolg von Boosting liegt in seinem iterativen Trainingsprozess, der sich systematisch auf die Fehler der Vorgängermodelle konzentriert.

  1. Start: Der Prozess beginnt mit einem ersten schwachen Lerner h1(x)h_1(x). Dieser Lerner trifft auf dem gesamten Datensatz Vorhersagen und wird unweigerlich Fehler machen.
  2. Fokussierung: Anstatt den nächsten Lerner h2(x)h_2(x) auf dem Originaldatensatz zu trainieren, wird der Datensatz oder, im Falle des Gradient Boostings, die Zielvariable für den nächsten Durchgang modifiziert. Dies geschieht, indem den Datenpunkten, die vom vorherigen Modell falsch klassifiziert oder schlecht vorhergesagt wurden, eine höhere Gewichtung zugewiesen wird (wie bei AdaBoost) oder indem die Restfehler (Residuen) des Vorgängers zur Zielgröße des neuen Modells werden (wie bei Gradient Boosting).
  3. Iteration: Jeder nachfolgende Lerner hm(x)h_m(x) wird speziell darauf trainiert, die Schwächen und Fehler des aktuellen Gesamtmodells Fm−1(x)F_{m-1}(x) zu beheben. Man könnte sagen, der neue Lerner lernt aus den Versäumnissen seiner Vorgänger.

Am Ende des Prozesses liegen MM einzelne, schwache Lerner vor. Der finale starke Lerner FM(x)F_M(x) wird durch eine gewichtete Summe oder Linearkombination dieser schwachen Lerner gebildet:

FM(x)=∑m=1Mαm⋅hm(x)F_M(x) = \sum_{m=1}^{M} \alpha_m \cdot h_m(x)

Wobei:

  • hm(x)h_m(x) der mm-te schwache Lerner (oft ein kleiner Entscheidungsbaum, auch Stump genannt) ist.
  • αm\alpha_m die Gewichtung dieses Lerners im finalen Ensemble darstellt. Lerner, die bei den schwierigeren (hoch gewichteten) Fällen eine bessere Leistung erbracht haben, erhalten ein höheres αm\alpha_m, also mehr Einfluss auf die Gesamtentscheidung.

Durch diese sequenzielle und fehlerorientierte Konstruktion ist das resultierende Ensemble FM(x)F_M(x) in der Lage, auch komplexe Zusammenhänge präzise abzubilden. Der Schlüssel ist die minimale Fehlerakkumulation: Jeder Schritt korrigiert einen Teil des noch bestehenden Fehlers, was insgesamt zu einem Modell mit sehr hoher Vorhersagegenauigkeit führt, das die Fehler der ursprünglichen schwachen Lerner effektiv minimiert und vermeidet.

Der Gradient Boosting Algorithmus

Gradient Boosting ist ein Additive-Modelle-Verfahren, das eine Funktion

F(x)=∑m=0Mν fm(x)F(x) = \sum_{m=0}^M \nu \, f_m(x)

aus vielen einfachen Basisfunktionen fmf_m konstruiert.

Für Regressionsaufgaben mit quadratischer Lossfunktion handelt es sich im Kern um einen Gradientenabstieg im Funktionsraum. Jeder neue Baum approximiert den negativen Gradienten der Lossfunktion. Das hier dargestellte Material basiert inhaltlich auf Masui (2022) [masui2022] und geht mathematisch weit über den Originalartikel hinaus.

Wir betrachten Trainingsdaten

{(xi,yi)}i=1n⊂Rd×R.\{(x_i, y_i)\}_{i=1}^n \subset \mathbb{R}^d \times \mathbb{R}.

Wir suchen ein Modell F(x)F(x), das die quadratische Lossfunktion minimiert:

L(F)=∑i=1n(yi−F(xi))2.\mathcal{L}(F) = \sum_{i=1}^n (y_i - F(x_i))^2.

Gradient Boosting nähert FF schrittweise durch additive Funktionen an:

Fm(x)=Fm−1(x)+ν fm(x),F_m(x) = F_{m-1}(x) + \nu \, f_m(x),

wobei ν∈(0,1]\nu \in (0,1] die Lernrate ist und fmf_m typischerweise ein Regressionsbaum.

Für eine allgemeine Lossfunktion L(y,F)\mathcal{L}(y, F) lautet der Gradient-Boosting-Algorithmus (Friedman, 2001):

Algorithmus: Gradient Boosting

  1. Initialisiere

    F0=arg⁡min⁡γ∑i=1nL(yi,γ).F_0 = \arg\min_\gamma \sum_{i=1}^n \mathcal{L}(y_i, \gamma).

  2. Für m=1,…,Mm = 1, \dots, M: a. Berechne die negativen Gradienten (Pseudo-Residuals) ri,m=−∂L(yi,F)∂F∣F=Fm−1(xi). r_{i,m} = -\left.\frac{\partial \mathcal{L}(y_i, F)}{\partial F}\right|_{F = F_{m-1}(x_i)}.

    b. Fit eines Regressionsbaums auf die Residuen: fm=FitTree(xi,ri,m). f_m = \text{FitTree}(x_i, r_{i,m}).

    c. Für jedes Blatt jj bestimme γj,m=arg⁡min⁡γ∑xi∈Rj,mL(yi,Fm−1(xi)+γ). \gamma_{j,m} = \arg\min_\gamma \sum_{x_i \in R_{j,m}} \mathcal{L}(y_i, F_{m-1}(x_i) + \gamma).

    d. Update Fm(x)=Fm−1(x)+ν∑j=1Jmγj,m 1{x∈Rj,m}. F_m(x) = F_{m-1}(x) + \nu \sum_{j=1}^{J_m} \gamma_{j,m}\,\mathbf{1}_{\{x \in R_{j,m}\}}.

Im Folgenden leiten wir diese Schritte für die quadratische Lossfunktion vollständig her.

Herleitung der Formeln für einen Regressions-Tree mit quadratischer Verlustfunktion (L2)

Wir wollen folgendes zeigen: Bei L2-Regression sind die Blattwerte Mittelwerte der Residuen.

Wir minimieren

F0=arg⁡min⁡γ∑i=1n(yi−γ)2.F_0 = \arg\min_\gamma \sum_{i=1}^n (y_i - \gamma)^2.

Ableitung:

∂∂γ∑i=1n(yi−γ)2=−2∑i=1n(yi−γ)=0.\frac{\partial}{\partial \gamma}\sum_{i=1}^n (y_i - \gamma)^2 = -2\sum_{i=1}^n (y_i - \gamma) = 0.

Daraus folgt:

γ=1n∑i=1nyi=yˉ.\gamma = \frac{1}{n} \sum_{i=1}^n y_i = \bar y.

Fazit: Bei L2-Regression ist F0F_0 gerade der Mittelwert der Response yy.

Wir berechnen die Pseudo-Residuals

ri,m=−∂(yi−F)2∂F=2(yi−Fm−1(xi)).r_{i,m} = -\frac{\partial (y_i - F)^2}{\partial F} = 2(y_i - F_{m-1}(x_i)).

Bis auf den Faktor 22 gilt:

ri,m=yi−Fm−1(xi),r_{i,m} = y_i - F_{m-1}(x_i),

also genau der Residuumvektor. Für jedes Blatt Rj,mR_{j,m} minimieren wir:

γj,m=arg⁡min⁡γ∑xi∈Rj,m(yi−(Fm−1(xi)+γ))2.\gamma_{j,m} = \arg\min_\gamma \sum_{x_i \in R_{j,m}} (y_i - (F_{m-1}(x_i) + \gamma))^2.

Ableitung:

∂∂γ∑(yi−Fm−1(xi)−γ)2=−2∑xi∈Rj,m(yi−Fm−1(xi)−γ).\frac{\partial}{\partial \gamma} \sum (y_i - F_{m-1}(x_i) - \gamma)^2 = -2 \sum_{x_i \in R_{j,m}} (y_i - F_{m-1}(x_i) - \gamma).

Setzen wir gleich Null:

∑(yi−Fm−1(xi)−γ)=0.\sum (y_i - F_{m-1}(x_i) - \gamma) = 0.

Damit:

γj,m=1∣Rj,m∣∑xi∈Rj,mri,m.\gamma_{j,m} = \frac{1}{|R_{j,m}|} \sum_{x_i \in R_{j,m}} r_{i,m}.

Interpretation als Gradientenabstieg

Ein wesentlicher theoretischer Zugang zu Gradient Boosting besteht darin, den Algorithmus nicht primär als Ensembleverfahren zu betrachten, sondern als eine Form des Gradientenabstiegs im Funktionsraum. Dieser Blickwinkel erlaubt eine präzise mathematische Beschreibung des Verfahrens und erklärt zugleich, weshalb Gradient Boosting in so vielen praktischen Anwendungen eine aussergewöhnlich hohe Leistung erzielt.

Wir betrachten den Raum aller reellwertigen Funktionen, die Eingaben aus Rd\mathbb{R}^d auf reelle Zahlen abbilden:

F={F:Rd→R}.\mathcal{F} = \{ F : \mathbb{R}^d \to \mathbb{R} \}.

Jedes Modell, das wir in einer Regressionsaufgabe konstruieren, ist ein Element dieses Funktionsraumes. Unser Ziel besteht darin, eine Funktion F∈FF \in \mathcal{F} zu finden, die die vorgegebene Verlustfunktion minimiert. Für Trainingsdaten (xi,yi)(x_i, y_i) formulieren wir das Optimierungsproblem als

F∗=arg⁡min⁡F∈F∑i=1nL(yi,F(xi)).F^\ast = \arg\min_{F \in \mathcal{F}} \sum_{i=1}^n L(y_i, F(x_i)).

Im Gegensatz zu klassischen Optimierungsverfahren, die Parametervektoren aktualisieren, führt Gradient Boosting eine Optimierung über Funktionen durch. Dies bedeutet, dass wir nicht an einem endlichen Parametervektor arbeiten, sondern an einer unendlichdimensionalen Struktur – einem Raum von Funktionen.

Der Gradient der Lossfunktion im Funktionsraum ist ein Objekt, das an jedem Trainingspunkt xix_i eine Richtung angibt, in die die Modellfunktion FF verändert werden sollte, um den Wert der Lossfunktion am stärksten zu verringern. Dieser funktionale Gradient wird durch die partiellen Ableitungen

∂L(yi,F(xi))∂F∣F=Fm−1\left.\frac{\partial L(y_i, F(x_i))}{\partial F}\right|_{F = F_{m-1}}

beschrieben und bildet einen Vektor im diskreten Raum der Trainingspunkte.

Gradient Boosting konstruiert nun schrittweise eine Modellfolge {Fm}m=0M\{F_m\}_{m=0}^M, indem es in jeder Iteration einen Schritt in Richtung des negativen Gradienten ausführt:

Fm=Fm−1−ν ∇FL(Fm−1).F_m = F_{m-1} - \nu \, \nabla_F L(F_{m-1}).

Hierbei bezeichnet ν>0\nu > 0 die Lernrate, welche die Grösse des Schrittes im Funktionsraum kontrolliert. Je kleiner die Lernrate gewählt wird, desto feiner sind die Korrekturen, die das Modell pro Iteration durchführt.

Approximation des funktionalen Gradienten durch Entscheidungsbäume

Ein zentrales Problem besteht darin, dass wir den funktionalen Gradient nicht direkt als Funktion auswerten können: Wir kennen den Gradienten nur an den diskreten Trainingspunkten xix_i. Ein echter Gradient im Funktionsraum wäre jedoch eine Funktion über dem gesamten Definitionsbereich.

Gradient Boosting löst dieses Problem elegant, indem es eine Funktion fm∈Ff_m \in \mathcal{F} konstruiert, die die Werte des negativen Gradienten an den Trainingspunkten so gut wie möglich approximiert:

fm(xi)≈−∂L(yi,F)∂F∣F=Fm−1(xi).f_m(x_i) \approx - \left.\frac{\partial L(y_i, F)}{\partial F}\right|_{F = F_{m-1}(x_i)}.

Die entscheidende Idee lautet:

Diese approximierende Funktion fmf_m wird durch einen Regressionsbaum dargestellt.

Regressionsbäume sind in der Lage, komplexe und nichtlineare Abhängigkeiten abzubilden, und eignen sich daher hervorragend als Approximation des Gradientenvektors. Da jeder Baum nur eine grobe Schätzung liefert, entsteht durch das sukzessive Hinzufügen vieler kleiner Bäume ein immer präziseres Modell. Aus dieser Perspektive lässt sich die Grundidee des Algorithmus zusammenfassen als:

Gradient Boosting=Gradientenabstieg im Funktionsraum.\text{Gradient Boosting} \quad = \quad \text{Gradientenabstieg im Funktionsraum}.

Jeder Boosting-Schritt fügt dem aktuellen Modell Fm−1F_{m-1} eine neue Funktion fmf_m hinzu, welche die Richtung des negativen Gradienten approximiert. Damit entsteht schrittweise ein immer besseres Modell, das dem wahren Minimierer der Lossfunktion näher kommt. Diese Sichtweise erklärt nicht nur die theoretische Fundierung des Verfahrens, sondern auch dessen praktische Stärke: Gradient Boosting kombiniert die Robustheit des Gradientenabstiegs mit der Flexibilität nichtlinearer Funktionsapproximation durch Entscheidungsbäume.

Python-Code

Datensimulation

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
x = np.linspace(0, 10, 80)
y = 3*np.sin(x) + 0.5*x + np.random.normal(0, 0.4, len(x))

plt.scatter(x, y)
plt.title("Datensimulation")
plt.show()

Stump Regressor

from dataclasses import dataclass

@dataclass
class Stump:
    thr: float = 0.0
    left: float = 0.0
    right: float = 0.0
    
    def fit(self, x, y):
        order = np.argsort(x)
        xs = x[order]; ys = y[order]
        best_loss = 1e99
        
        for i in range(1, len(xs)):
            t = 0.5*(xs[i-1] + xs[i])
            left = ys[xs < t].mean() if np.any(xs < t) else 0
            right = ys[xs >= t].mean() if np.any(xs >= t) else 0
            pred = np.where(xs < t, left, right)
            loss = ((pred - ys)**2).sum()
            if loss < best_loss:
                best_loss = loss
                self.thr, self.left, self.right = t, left, right
        
    def predict(self, x):
        return np.where(x < self.thr, self.left, self.right)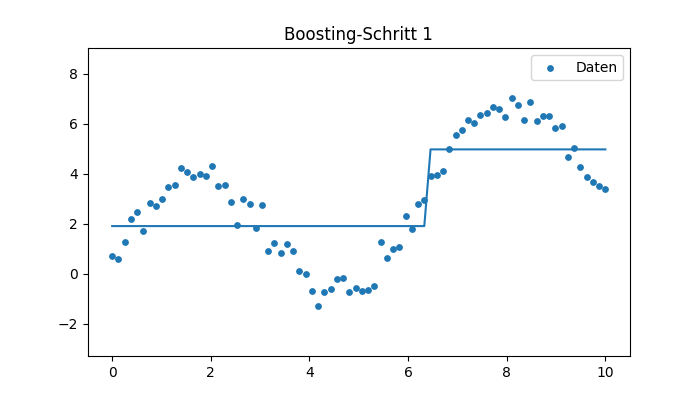

Boosting Schritt 1

Gradient Boosting

def boost(x, y, M=5, lr=0.3):
    F = np.full_like(y, y.mean())
    models = []
    for _ in range(M):
        r = y - F
        stump = Stump()
        stump.fit(x, r)
        F = F + lr * stump.predict(x)
        models.append(stump)
    return F, models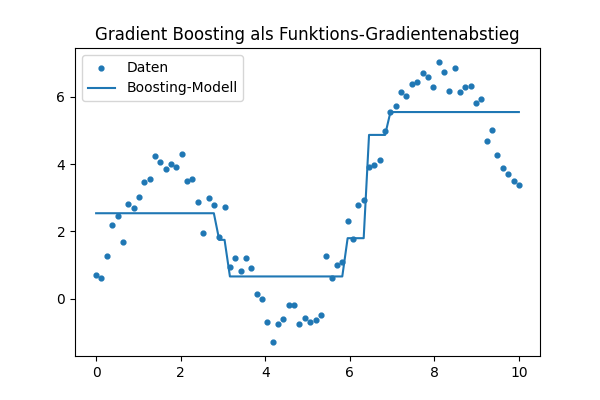

Gradient Boosting Regressor nach der 5. Iteration

Visualisierung der Boosting-Schritte

F_pred, models = boost(x, y, M=6, lr=0.3)
F = np.full_like(y, y.mean())
steps = [F.copy()]

for stump in models:
    F = F + 0.3 * stump.predict(x)
    steps.append(F.copy())
    
for i, Fm in enumerate(steps):
    plt.plot(x, Fm, label=f"Iteration {i}")

plt.scatter(x, y, s=10)
plt.legend()
plt.title("Gradient Boosting Schritte")
plt.show()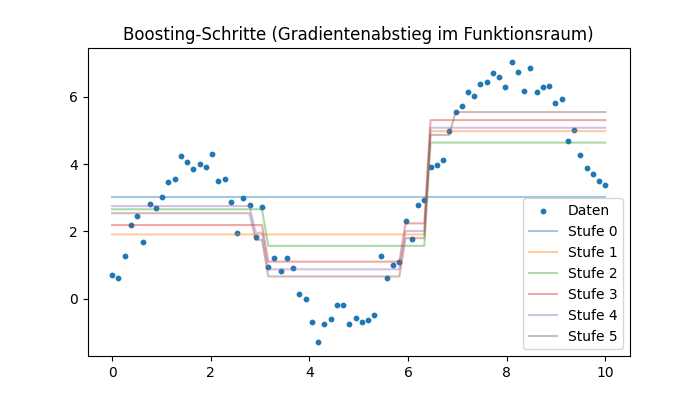

Alle 5 Boosting-Schritte zusammen

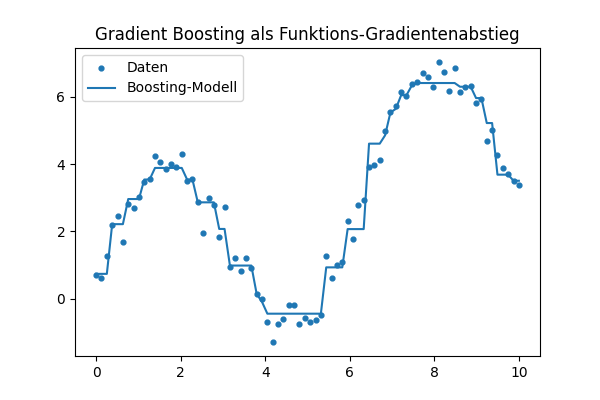
Gradient Boosted Tree nach 50 Iterationen

Fazit

Die Herleitung des Gradient-Boosting-Algorithmus zeigt sehr schön, wie eng dieses Verfahren mit der Idee des Gradientenabstiegs verknüpft ist. Während beim klassischen Gradientenabstieg Parameter eines einzigen Modells optimiert werden, arbeitet Gradient Boosting auf einer höheren Ebene: Der Algorithmus führt einen Gradientenabstieg im Funktionsraum durch. Das bedeutet, dass nicht Parameter, sondern ganze Funktionen schrittweise aktualisiert werden. Jede neue Funktion – typischerweise ein kleiner Entscheidungsbaum – wirkt dabei wie ein Korrekturschritt, der die bestehende Modellfunktion in Richtung des negativen Gradienten der Lossfunktion verschiebt.

Für die häufig verwendete L2-Regression lässt sich besonders klar erkennen, wie dieser Mechanismus funktioniert. Der funktionale Gradient der quadratischen Verlustfunktion entspricht exakt den Residuen zwischen Modellvorhersage und Zielwert. Das bedeutet: In jedem Boosting-Schritt wird ein Regressionsbaum an jene Werte angepasst, die das aktuelle Modell noch nicht erklären kann. Diese Residuen repräsentieren also direkt den ”Fehler”, in dessen Richtung sich das Modell verbessern muss. Die Blattwerte des Regressionsbaums – also die vorhergesagten Korrekturwerte in jedem Teilraum – ergeben sich als Mittelwerte der Residuen in den entsprechenden Regionen. Auf diese Weise liefern die Bäume lokal passende Korrekturen, die das Modell präzise weiterentwickeln.

Eine weitere wichtige Eigenschaft ist die Rolle der Lernrate (learning rate). Sie bestimmt die Grösse des jeweiligen Schritts im Funktionsraum und verhindert, dass das Modell zu grosse, instabile Korrekturen vornimmt. Kleine Lernraten führen zwar zu mehr benötigten Iterationen, ermöglichen aber zugleich feinere Anpassungen und reduzieren typischerweise das Risiko des Überfittings. Gradient Boosting ist deshalb nicht nur ein schrittweises, sondern auch ein kontrolliertes Verbesserungsverfahren.

Diese Kombination aus funktionalem Gradientenabstieg, residuenbasierten Korrekturen und fein steuerbaren Schrittweiten macht Gradient Boosting zu einer der leistungsfähigsten Methoden des überwachten Lernens. Besonders stark ist das Verfahren bei tabellarischen, heterogenen oder nichtlinear strukturierten Daten, wo lineare Modelle oder tiefere neuronale Netze häufig an ihre Grenzen stossen. Moderne Varianten wie XGBoost, LightGBM oder CatBoost erweitern diese Grundidee um Regularisierung, effiziente Implementierungen und weitere Optimierungen – und erreichen damit in vielen praktischen Anwendungen State-of-the-Art-Ergebnisse.

Gradient Boosting wird heute erfolgreich eingesetzt in Aufgaben wie der Vorhersage von Immobilienpreisen, im Risikoscoring im Finanzwesen, bei Zeitreihen mit nichtlinearen Effekten, in der medizinischen Diagnostik sowie allgemein überall dort, wo robuste, hochperformante Modelle für strukturierte Daten benötigt werden. Die theoretische Eleganz und die praktische Leistungsfähigkeit machen Gradient Boosting zu einem der zentralen Werkzeuge im Werkzeugkasten des modernen Machine Learnings.

Anhang: Funktionale Ableitung und geometrische Interpretation

In diesem Abschnitt leiten wir die funktionale Ableitung (den Gradienten im Funktionsraum) für das empirische Risiko explizit her und geben anschliessend eine geometrische Interpretation. Der zentrale Punkt ist, dass sich Gradient Boosting als Gradientenabstieg in einem (endlichen) Funktionsraum interpretieren lässt, in dem die Funktionswerte auf den Trainingspunkten die Rolle von Koordinaten spielen.

Wir betrachten wie zuvor Trainingsdaten

{(xi,yi)}i=1n⊂Rd×R\{(x_i, y_i)\}_{i=1}^n \subset \mathbb{R}^d \times \mathbb{R}

und ein Modell F:Rd→RF : \mathbb{R}^d \to \mathbb{R}.

Das empirische Risiko definieren wir allgemein als

L(F)=∑i=1nL(yi,F(xi)),\mathcal{L}(F) = \sum_{i=1}^n L\bigl(y_i, F(x_i)\bigr),

wobei L(y,y^)L(y, \hat{y}) eine differenzierbare Verlustfunktion ist.

Wichtig ist nun die Beobachtung: Für die Optimierung auf den Trainingsdaten genügt es, die Funktionswerte

F(x1),F(x2),…,F(xn)F(x_1), F(x_2), \dots, F(x_n)

zu betrachten. Aus Sicht der Optimierung können wir also den Vektor

F=(F(x1)F(x2)⋮F(xn))∈Rn\mathbf{F} = \begin{pmatrix} F(x_1) \\ F(x_2) \\ \vdots \\ F(x_n) \end{pmatrix} \in \mathbb{R}^n

als die relevanten Parameter ansehen, auf denen das empirische Risiko tatsächlich beruht. Damit ist das Risiko eine Funktion

L:Rn→R,L(F)=∑i=1nL(yi,F(xi)).\mathcal{L} : \mathbb{R}^n \to \mathbb{R}, \qquad \mathcal{L}(\mathbf{F}) = \sum_{i=1}^n L\bigl(y_i, F(x_i)\bigr).

Die (diskrete) Gradientenableitung nach den Komponenten F(xi)F(x_i) ist dann

∂L∂F(xi)=∂∂F(xi)L(yi,F(xi)),\frac{\partial \mathcal{L}}{\partial F(x_i)} = \frac{\partial}{\partial F(x_i)} L \bigl(y_i, F(x_i) \bigr),

da jeder Summand L(yj,F(xj))L(y_j, F(x_j)) für j≠ij \neq i unabhängig von F(xi)F(x_i) ist. Der Gradient von L\mathcal{L} bezüglich der Funktionswerte ist also der Vektor

∇L(F)=(∂L∂F(x1)∂L∂F(x2)⋮∂L∂F(xn))=(∂∂F(x1)L(y1,F(x1))∂∂F(x2)L(y2,F(x2))⋮∂∂F(xn)L(yn,F(xn))).\nabla \mathcal{L}(F) = \begin{pmatrix} \dfrac{\partial \mathcal{L}}{\partial F(x_1)} \\ \dfrac{\partial \mathcal{L}}{\partial F(x_2)} \\ \vdots \\ \dfrac{\partial \mathcal{L}}{\partial F(x_n)} \end{pmatrix} = \begin{pmatrix} \dfrac{\partial}{\partial F(x_1)} L\bigl(y_1, F(x_1)\bigr) \\ \dfrac{\partial}{\partial F(x_2)} L\bigl(y_2, F(x_2)\bigr) \\ \vdots \\ \dfrac{\partial}{\partial F(x_n)} L\bigl(y_n, F(x_n)\bigr) \end{pmatrix}.

Dies ist genau der Vektor der partiellen Ableitungen der Lossfunktion nach den Funktionswerten. Für die in der Regression sehr häufig verwendete quadratische Lossfunktion

L(y,y^)=(y−y^)2L(y, \hat{y}) = (y - \hat{y})^2

ergibt sich für einen einzelnen Summanden

L(yi,F(xi))=(yi−F(xi))2.L\bigl(y_i, F(x_i)\bigr) = \bigl(y_i - F(x_i)\bigr)^2.

Die Ableitung nach F(xi)F(x_i) ist

∂∂F(xi)(yi−F(xi))2=2(yi−F(xi))⋅∂∂F(xi)(yi−F(xi)).\frac{\partial}{\partial F(x_i)} \bigl(y_i - F(x_i)\bigr)^2 = 2\bigl(y_i - F(x_i)\bigr)\cdot \frac{\partial}{\partial F(x_i)}(y_i - F(x_i)).

Da yiy_i konstant ist und ∂∂F(xi)(−F(xi))=−1\frac{\partial}{\partial F(x_i)}(-F(x_i)) = -1, erhalten wir

∂∂F(xi)(yi−F(xi))2=−2(yi−F(xi)).\frac{\partial}{\partial F(x_i)} \bigl(y_i - F(x_i)\bigr)^2 = -2\bigl(y_i - F(x_i)\bigr).

Damit ist die partielle Ableitung des empirischen Risikos

=∂∂F(xi)∑j=1n(yj−F(xj))2=−2(yi−F(xi)),= \frac{\partial}{\partial F(x_i)} \sum_{j=1}^n (y_j - F(x_j))^2 = -2\bigl(y_i - F(x_i)\bigr),

da alle Terme mit j≠ij \neq i keine Funktion von F(xi)F(x_i) sind. Der Gradientvektor ist also

∇L(F)=−2(y1−F(x1)y2−F(x2)⋮yn−F(xn)).\nabla \mathcal{L}(F) = -2 \begin{pmatrix} y_1 - F(x_1) \\ y_2 - F(x_2) \\ \vdots \\ y_n - F(x_n) \end{pmatrix}.

Die negative Gradientenrichtung ist damit proportional zum Residuenvektor

r=(y1−F(x1)y2−F(x2)⋮yn−F(xn)).\mathbf{r} = \begin{pmatrix} y_1 - F(x_1) \\ y_2 - F(x_2) \\ \vdots \\ y_n - F(x_n) \end{pmatrix}.

Bis auf einen konstanten Faktor 22 gilt also:

−∇L(F)∝r.-\nabla \mathcal{L}(F) \propto \mathbf{r}.

Für L2-Regression ist der negative Gradient des empirischen Risikos genau der Vektor der Residuen. Wenn Gradient Boosting also einen Baum auf den Pseudo-Residuen fittet bedeutet, heisst das konkret: Der Baum approximiert den negativen Gradienten der Lossfunktion im Raum der Funktionswerte.

Funktionale Sichtweise

Die obige Herleitung war bewusst diskret und endlichdimensional. In einer etwas abstrakteren (funktionalanalytischen) Sichtweise betrachten wir den Funktionsraum

F=F:Rd→R\mathcal{F} = { F : \mathbb{R}^d \to \mathbb{R} }

als einen Vektorraum, in dem sich Funktionen addieren und mit Skalaren multiplizieren lassen. Das empirische Risiko L\mathcal{L} wird dann zu einem Funktional

L:F→R.\mathcal{L} : \mathcal{F} \to \mathbb{R}.

Die funktionale Ableitung von L\mathcal{L} an der Stelle FF ist ein Objekt, das jedem Punkt xx (oder zumindest jedem Trainingspunkt xix_i) einen Ableitungswert zuordnet. Anschaulich gibt die funktionale Ableitung an, wie sich L\mathcal{L} ändert, wenn man FF in Richtung einer kleinen Störung δF\delta F verändert.

Formal betrachtet man dazu eine Variation F+εhF + \varepsilon h mit einem Richtungsfeld hh und kleinem ε\varepsilon. Die erste Variation von L\mathcal{L} in Richtung hh ist durch

δL(F;h)=ddε∣ε=0L(F+εh)\delta \mathcal{L}(F; h) = \left.\frac{d}{d \varepsilon}\right|_{\varepsilon=0} \mathcal{L}(F + \varepsilon h)

gegeben. Im diskreten Fall reduziert sich dies auf

δL(F;h)=∑i=1n∂L∂F(xi) h(xi).\delta \mathcal{L}(F; h) = \sum_{i=1}^n \frac{\partial \mathcal{L}}{\partial F(x_i)} \, h(x_i).

Steht uns ein Skalarprodukt ⟨⋅,⋅⟩\langle \cdot, \cdot \rangle auf dem Funktionsraum (oder im diskreten Fall auf Rn\mathbb{R}^n) zur Verfügung, so lässt sich die erste Variation auch schreiben als

δL(F;h)=⟨∇L(F),,h⟩,\delta \mathcal{L}(F; h) = \bigl\langle \nabla \mathcal{L}(F),, h \bigr\rangle,

wobei ∇L(F)\nabla \mathcal{L}(F) nun als Gradient im Funktionsraum aufgefasst wird. Die Gleichung zeigt: Der Gradient ist genau das Objekt, das in jeder Richtung hh die Richtungsableitung liefert.

Geometrische Interpretation

Die geometrische Interpretation von Gradient Boosting folgt direkt aus dieser Gradientsicht.

  • Raum der Funktionswerte. Im diskreten Setting auf den Trainingsdaten können wir das Modell FF mit seinem Vektor der Funktionswerte F=(F(x1),…,F(xn))⊤\mathbf{F} = (F(x_1), \dots, F(x_n))^\top identifizieren. Dieser Vektor lebt in einem nn-dimensionalen euklidischen Raum Rn\mathbb{R}^n.

  • Gradient als Steilsteigungsrichtung. Der Gradient ∇L(F)\nabla \mathcal{L}(F) ist die Richtung, in der die Lossfunktion am stärksten ansteigt. Die negative Gradientenrichtung −∇L(F)-\nabla \mathcal{L}(F) ist dementsprechend die Richtung des stärksten Abstiegs.

  • Gradientenabstieg. Ein klassischer Gradientenabstieg im Vektorraum Rn\mathbb{R}^n könnte als Update schreiben:

    Fm=Fm−1−ν,∇L(Fm−1).\mathbf{F}_m = \mathbf{F}_{m-1} - \nu , \nabla \mathcal{L}(\mathbf{F}_{m-1}).

    Im Funktionsraum formuliert man dies symbolisch als

    Fm=Fm−1−ν,∇FL(Fm−1),F_m = F_{m-1} - \nu , \nabla_F \mathcal{L}(F_{m-1}),

    was genau die Notation ist, die häufig im Kontext von Gradient Boosting verwendet wird.

  • Rolle der Bäume. In der Praxis können wir nicht beliebige Funktionsänderungen δF\delta F wählen, sondern sind auf Funktionen beschränkt, die durch Regressionsbäume darstellbar sind. Jeder Baum fmf_m stellt also eine approximative Projektion des negativen Gradienten auf den Raum der Baumfunktionen dar:

    fm≈−∇FL(Fm−1).f_m \approx - \nabla_F \mathcal{L}(F_{m-1}).

    Das Update

    Fm=Fm−1+νfmF_m = F_{m-1} + \nu f_m

    bedeutet geometrisch: Wir bewegen uns von Fm−1F_{m-1} aus in einer Richtung, die möglichst gut mit der Richtung des stärksten Abstiegs übereinstimmt, jedoch innerhalb der erlaubten Modellklasse der Bäume liegt.

  • Schrittweite und Lernrate. Die Lernrate ν\nu skaliert die Schrittweite. Geometrisch bestimmt sie, wie weit wir in Richtung des approximierten Gradienten gehen. Kleine Lernraten führen zu vielen kleinen Schritten, grosse Lernraten zu wenigen grossen Schritten.

Gradient Boosting kann geometrisch als schrittweiser Abstieg auf der Losslandschaft interpretiert werden, wobei die Position durch die Funktionswerte F(xi)F(x_i) repräsentiert wird und die Abstiegsrichtung durch den (negativen) Gradienten der Lossfunktion gegeben ist. Regressionsbäume dienen dabei als begrenzte, aber flexible Basisfunktionen, mit denen diese Abstiegsrichtung in jeder Iteration approximiert wird. Dadurch entsteht ein algorithmisch realisierbarer Gradientenabstieg im Funktionsraum.

Referenzen