From Vectors to Graphs: The Evolution of Retrieval-Augmented Generation
From Vectors to Graphs: The Evolution of Retrieval-Augmented Generation
Christoph Würsch, Institute for Computational Engineering, ICE, OST
Table of Contents
- Introduction to RAG Systems
- Graph RAG Architecture
- Retrieval Modalities
- Hierarchical Clustering and the Leiden Algorithm
- Code Example
Standard Retrieval-Augmented Generation (RAG) systems rely heavily on vector embeddings to retrieve relevant context. While effective for local semantic queries, these systems often fail to capture global structural information and multi-hop relationships across large corpora. This article introduces Graph RAG, a paradigm shift that integrates Knowledge Graphs (KGs) into the retrieval pipeline. We explore the architectural differences, the mathematical formulation of graph-based retrieval, and the Community Summary approach for global reasoning.
You can donwload pdf-version of the article here
1. Introduction to RAG Systems
Large Language Models (LLMs) are powerful reasoning engines, but they suffer from two critical limitations: they are “frozen in time” (limited to their training data cutoff) and they lack access to proprietary or private knowledge. Retrieval-Augmented Generation (RAG) is a hybrid architecture designed to bridge this gap.
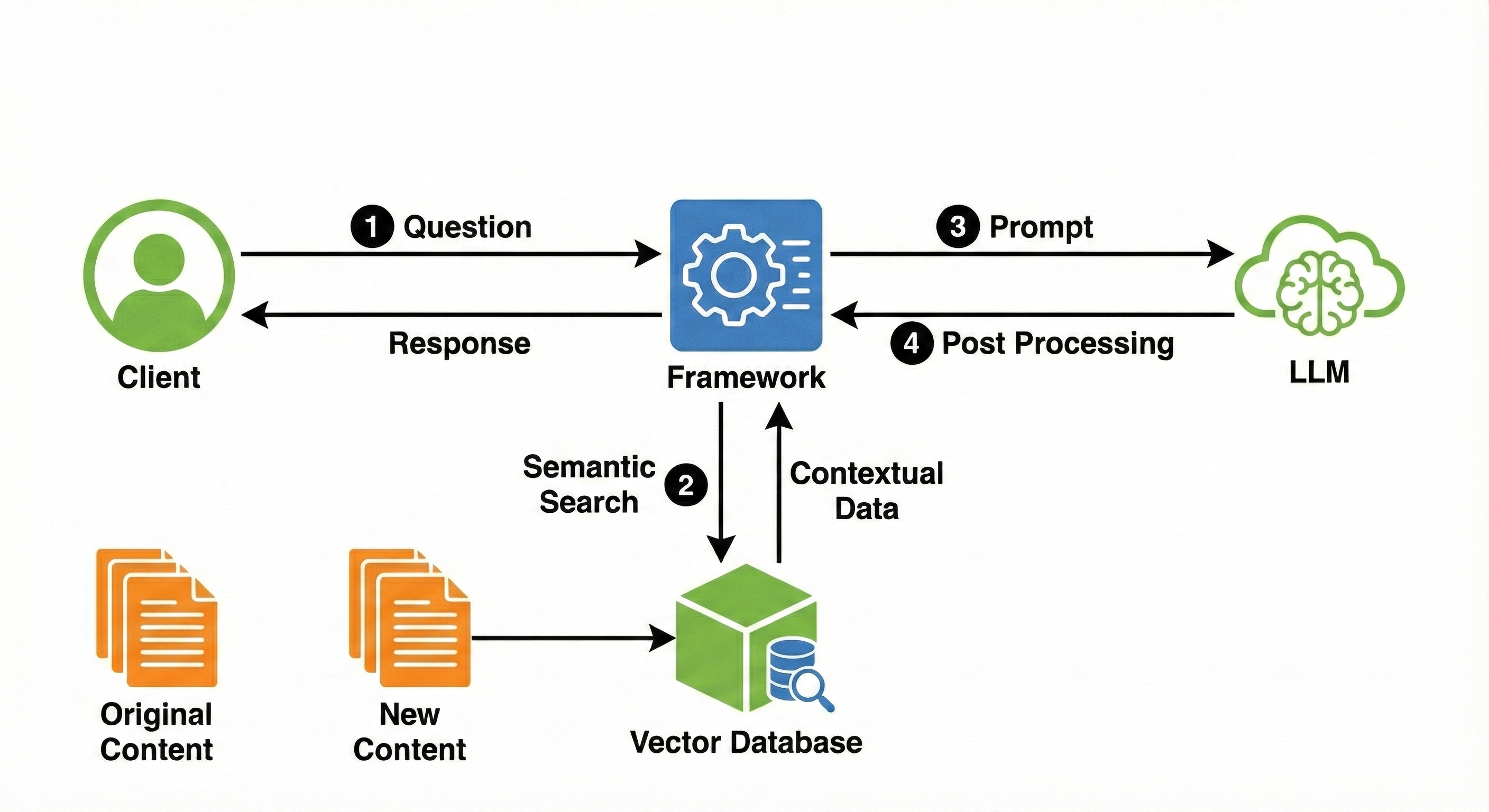
RAG fundamentally alters the interaction with an LLM by shifting from a purely generative paradigm to a Retrieve-then-Generate workflow. When a user submits a query, the system does not immediately send it to the LLM. Instead, it first acts as an intelligent librarian, searching a vast dataset to retrieve relevant text chunks. These chunks are then appended to the original query as “context.” The LLM is instructed to answer the question using only the provided information, thereby grounding the response in factual data and significantly reducing hallucinations.
To retrieve relevant information, the system must understand the “meaning” of both the user’s query and the stored documents. Since computers cannot inherently understand language, we must translate text into a mathematical format. This is achieved through an Embedding Model, a neural network trained to map discrete text inputs into continuous numerical representations.
Formally, an embedding function transforms a text sequence into a vector within a high-dimensional vector space :
The dimensionality is typically high (e.g., 768 or 1536 dimensions), allowing the model to capture subtle nuances of language.
The resulting vector space is semantic, meaning that the geometric position of a vector encodes its conceptual meaning. In this space, distance correlates with semantic relatedness. For example, the mathematical vector for “Apple” will be positioned closer to “Fruit” and “Technology” than to “Car,” depending on the context. This allows the system to identify relevant documents even if they do not share the exact keywords as the query, a significant improvement over traditional keyword search.
Once the query and the documents are mapped to this high-dimensional space, the retrieval task becomes a geometry problem. We need to find the document vectors that are “closest” to the query vector.
While Euclidean distance is common in 2D space, it is often suboptimal for text embeddings because the magnitude (length) of the vector can be affected by the length of the text chunk. Instead, we use Cosine Similarity, which measures the cosine of the angle between two vectors. This metric focuses purely on the orientation of the vectors—i.e., whether they are pointing in the same semantic direction.
Given a query vector and a document vector , the similarity is calculated as:
A result of indicates identical semantic meaning (vectors overlap), while a result of indicates orthogonality (completely unrelated concepts).
1.1 Scalability and Fast Vector Search
In a production environment containing millions or billions of text chunks, calculating the Cosine Similarity between the query and every stored vector (a linear scan, ) is computationally prohibitive. To achieve low-latency retrieval, we employ Approximate Nearest Neighbor (ANN) algorithms. The industry standard for this is HNSW (Hierarchical Navigable Small World). Rather than scanning every point, HNSW organizes vectors into a multi-layered graph structure, analogous to a map with both highways and local roads.
- The algorithm begins at the top layers (“highways”), where connections are sparse and span long distances, allowing the search to quickly traverse the vector space to the general neighborhood of the query.
- Once in the vicinity, the algorithm descends to lower layers (“local roads”), where connections are dense, enabling a precise search for the exact nearest neighbors.
This hierarchical approach reduces the search complexity from linear time to logarithmic time (), enabling the retrieval of the most semantically relevant information from massive datasets in milliseconds.
1.2 The Limitations of Baseline RAG
In a standard RAG pipeline, a corpus is split into chunks . An embedding model maps these chunks to a vector space . Retrieval is performed via Approximate Nearest Neighbor (ANN) search:
Similarity
where is the query. This approach suffers from two primary deficits:
- Context Fragmentation: The model loses the connection between chunk and chunk if they are not semantically similar, even if they are logically related (e.g., via a causal chain).
- Lack of Global Overview: Vector RAG cannot effectively answer holistic questions (e.g., What are the changing political themes in this dataset?) because the answer is not contained in any single chunk.
2. Graph RAG Architecture
Graph RAG augments the retrieval process by constructing a directed graph from the source text, where represents entities and represents relationships.
2.1 The Indexing Phase: LLM-Driven Topology Construction
The indexing phase in Graph RAG represents a significant departure from the computationally lightweight embedding process of standard Vector RAG. While vector systems simply map text to numbers, Graph RAG acts as a structured reasoning engine that transforms unstructured text into a deterministic network topology. This process is heavily reliant on Large Language Models (LLMs) to function as intelligent extractors.
The process begins by dividing the corpus into chunks, similar to standard approaches. However, rather than immediately embedding these chunks, the system passes each text chunk to an LLM with a specific prompt instruction: identifying the core entities (nodes) and the relationships (edges) binding them. Unlike traditional Knowledge Graph construction, which often relies on rigid, pre-defined ontologies or fragile regular expressions, the LLM approach allows for an “open schema,” dynamically discovering entity types relevant to the specific domain.
Formally, for a given text chunk , the extraction function yields a set of triples:
where is the head entity (source), is the tail entity (target), and represents the specific semantic relationship between them.
However, a graph consisting solely of sparse triples (e.g., Einstein, studied, Physics) often fails to capture the richness of the source text. A strictly topological graph loses the subtle context of how or why a relationship exists. To address this, modern Graph RAG implementations (such as the methodology proposed by Microsoft Research) introduce a layer of natural language annotation.
In this enhanced indexing workflow, the LLM generates a dense natural language description, denoted as , for every identified node and edge. For example, rather than simply linking “Company A” to “Product B,” the edge attribute might contain a summary paragraph explaining that “Company A acquired the rights to Product B following a hostile takeover in 2023.” This hybrid approach preserves the nuanced semantic information that strict triples typically discard, ensuring that the graph retains the fidelity of the original text while providing the structural advantages of network analysis.
2.2 Hierarchical Clustering and Community Detection
To enable global search, the graph must be partitioned. We employ modularity-based community detection algorithms, such as the Leiden Algorithm.
Let be a partition of . The Leiden algorithm maximizes modularity :
Modularity
where is the adjacency matrix weight, is the degree of node , is the total edge weight, and is the Kronecker delta.
This process creates a hierarchical structure of communities. The system then uses an LLM to generate a summary for each community , creating a high-level index of the data’s topology.
3. Retrieval Modalities
Graph RAG introduces dual retrieval capabilities that standard RAG lacks.
3.1 Local Search (Multi-hop Reasoning)
For queries requiring specific details about an entity (e.g., How is Algorithm A related to Researcher B?), the system:
- Identifies entry nodes in based on query entities.
- Traverses edges (e.g., via Breadth-First Search or personalized PageRank) to find connected concepts hops away.
- Aggregates the text descriptions of the traversed path into the context window.
3.2 Global Search (Map-Reduce Summarization)
For broad queries (e.g., What are the main conflicts in the story?), standard RAG fails because the answer exists in the aggregate, not in a chunk. Graph RAG solves this by:
- Map: Selecting community summaries from the hierarchical level appropriate for the query’s granularity.
- Reduce: Feeding these summaries to the LLM to synthesize a global answer.
3.3 Computational Complexity and Trade-offs
While Graph RAG significantly improves sense-making capabilities, it introduces latency and cost.
| Metric | Standard RAG | Graph RAG |
|---|---|---|
| Indexing Cost | (Embedding) | (High) |
| Query Latency | Milliseconds (ANN Search) | Seconds (Graph Traversal/Map-Reduce) |
| Recall | High for explicit similarity | High for implicit/structural links |
Graph RAG represents the convergence of symbolic AI (Knowledge Graphs) and connectionist AI (LLMs). It addresses the reasoning gap in standard RAG. Future work involves Graph-Vector Hybrids, where retrieval is performed simultaneously in vector space and graph space to maximize both precision and breadth.
4. Hierarchical Clustering on Graphs and the Leiden Algorithm
To enable the Global Search capability—wherein the system answers queries regarding broad themes across the entire corpus—the Knowledge Graph must be organized into a semantic hierarchy. We achieve this through recursive modularity optimization. While the Louvain algorithm is a common standard, Graph RAG implementations prefer the Leiden Algorithm due to its guarantee of generating connected communities and its superior convergence speed.
4.1 Mathematical Formulation of Modularity
The objective function for community detection is the maximization of Modularity (). Modularity measures the density of links inside communities compared to links between communities.
For a weighted graph, Modularity is defined as:
Modularity
Where:
- represents the edge weight between nodes and .
- is the weighted degree of node .
- is the total edge weight in the graph.
- denotes the community to which node belongs.
- is the Kronecker delta function, equal to 1 if , and 0 otherwise.
The term represents the expected edge weight between nodes and in a random graph with the same degree distribution. Thus, we maximize the deviation of the actual graph structure from the null model.
4.2 The Leiden Algorithm Mechanics
The Leiden algorithm improves upon the Louvain method by addressing a critical flaw: Louvain can produce arbitrarily badly connected (or even disconnected) communities. Leiden introduces a Refinement Phase to guarantee connectivity. The algorithm iterates through three distinct phases:
Phase 1: Fast Local Moving
Similar to Louvain, this phase iterates through all nodes. For each node , we calculate the gain in modularity if were moved from its current community to the community of one of its neighbors.
Node is moved to the community that maximizes , provided .
Phase 2: Refinement
This is the distinguishing feature of Leiden. Instead of aggregating the communities directly from Phase 1, we refine them.
- Let be the partition found in Phase 1.
- The algorithm initializes a refined partition where every node is a singleton.
- It attempts to merge nodes in only if they belong to the same community in and are well-connected.
- This effectively splits the communities from Phase 1 into well-connected sub-communities.
Phase 3: Aggregation
The graph is coarsened based on . Each community in the refined partition becomes a single super-node in the new aggregate graph. Edges between super-nodes are weighted by the sum of weights of the edges between the constituent nodes.
4.3 Algorithmic Representation
The process is recursive. The output of the aggregation phase serves as the input for the next iteration, building the hierarchical levels required for Graph RAG (Level 0 Level 1 … Root).
Algorithm: Leiden Algorithm for Hierarchical Graph Partitioning
Require Graph G=(V,E)
Ensure Hierarchy of partitions H
1: G_current <- G
2: H <- empty set
3: While G_current is not sufficiently reduced
4: P_local <- SingletonPartition(G_current)
// Phase 1: Local Move
5: Repeat
6: For All v in V(G_current)
7: C_best <- argmax(C in Neighbors(v)) of Delta Q(v -> C)
8: If Delta Q > 0
9: Move v to C_best in P_local
10: End If
11: End For
12: Until Convergence
// Phase 2: Refinement
13: P_refined <- SingletonPartition(G_current)
14: For All v in V(G_current)
15: If v is well-connected within P_local(v)
16: Merge v into a cluster in P_refined within P_local(v)
17: (Selection based on randomized greedy optimization)
18: End If
19: End For
// Phase 3: Aggregation
20: G_next <- Aggregate(G_current, P_refined)
21: Add P_refined to H
22: G_current <- G_next
23: End While
24: Return H4.4 Relevance to Graph RAG Summarization
In the context of Graph RAG, the resulting hierarchy allows for Map-Reduce summarization:
- Leaf Communities (Level ): Contain granular details (e.g., specific interactions between two entities).
- Intermediate Communities (Level 1): Summarize groups of leaf communities (e.g., Conflict between Department A and B).
- Root Community (Level 0): Provides the global summary of the entire dataset.
5. Code Example
To demonstrate the hierarchical nature of Graph RAG (Level 0, Level 1, etc.) using the Leiden Algorithm, this code uses the resolution_parameter.
- High Resolution: Detects small, dense “Leaf” communities (local context).
- Low Resolution: Detects large, broad “Summary” communities (global context).
- Graph Generation (Stochastic Block Model): We generate a graph that mimics a real Knowledge Graph with clusters. In a real scenario, these clusters might represent topics like “Politics,” “Technology,” or “Healthcare.” The nodes within them are densely connected (related concepts), while connections between clusters are sparse.
leidenalg.RBConfigurationVertexPartition: This is the key line. We use the Reichardt-Bornholdt method, which is a variation of Modularity that accepts aresolution_parameter().
import networkx as nx
import igraph as ig
import leidenalg
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
def nx_to_igraph(nx_graph):
"""
Helper function to convert NetworkX graph to iGraph
(required because leidenalg is optimized for iGraph).
"""
# Relabel nodes to integers 0..N-1 for igraph consistency
mapping = {node: i for i, node in enumerate(nx_graph.nodes())}
H = nx.relabel_nodes(nx_graph, mapping)
g = ig.Graph(len(H), list(H.edges()))
return g, mapping
def plot_graph_partition(ax, G, partition_dict, title, pos):
"""
Visualizes the graph with nodes colored by their community.
"""
# Get unique communities and generate a color map
communities = set(partition_dict.values())
num_communities = len(communities)
cmap = cm.get_cmap('viridis', num_communities)
# Draw nodes
node_colors = [cmap(partition_dict[n]) for n in G.nodes()]
nx.draw_networkx_nodes(G, pos, node_size=100, node_color=node_colors, alpha=0.9, ax=ax)
nx.draw_networkx_edges(G, pos, alpha=0.2, ax=ax)
# Add title and stats
ax.set_title(f"{title}\n({num_communities} Communities)", fontsize=12, fontweight='bold')
ax.axis('off')
def run_leiden_demo():
# ---------------------------------------------------------
# 1. Setup: Generate a Synthetic "Knowledge Graph"
# ---------------------------------------------------------
print("Generating Stochastic Block Model Graph...")
# We create a graph with inherent structure:
# 5 clusters of 20 nodes, connected with probability 0.5 within, 0.02 between.
sizes = [20, 20, 20, 20, 20]
probs = [[0.5, 0.02, 0.02, 0.02, 0.02],
[0.02, 0.5, 0.02, 0.02, 0.02],
[0.02, 0.02, 0.5, 0.02, 0.02],
[0.02, 0.02, 0.02, 0.5, 0.02],
[0.02, 0.02, 0.02, 0.02, 0.5]]
G = nx.stochastic_block_model(sizes, probs, seed=42)
# Calculate layout once so nodes don't move between plots
pos = nx.spring_layout(G, seed=42, k=0.2)
# Convert to iGraph for the Leiden algorithm
G_ig, mapping = nx_to_igraph(G)
reverse_mapping = {v: k for k, v in mapping.items()}
# ---------------------------------------------------------
# 2. The Leiden Algorithm (Simulating Graph RAG Hierarchy)
# ---------------------------------------------------------
# SCENARIO A: High Resolution (Leaf Communities)
# This represents specific, granular topics (e.g., "Specific Causal Chain")
# RBConfigurationVertexPartition implements Modularity with resolution
part_leaf = leidenalg.find_partition(
G_ig,
leidenalg.RBConfigurationVertexPartition,
resolution_parameter=4.1
)
# SCENARIO B: Low Resolution (Root/Summary Communities)
# This represents the "Map-Reduce" global summary level
part_root = leidenalg.find_partition(
G_ig,
leidenalg.RBConfigurationVertexPartition,
resolution_parameter=0.3
)
# Convert igraph membership back to networkx dict format
# Format: {node_id: community_id}
dict_leaf = {reverse_mapping[i]: part_leaf.membership[i] for i in range(len(part_leaf.membership))}
dict_root = {reverse_mapping[i]: part_root.membership[i] for i in range(len(part_root.membership))}
# ---------------------------------------------------------
# 3. Visualization
# ---------------------------------------------------------
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# Plot 1: Raw Graph
nx.draw_networkx_nodes(G, pos, node_size=50, node_color='gray', alpha=0.5, ax=axes[0])
nx.draw_networkx_edges(G, pos, alpha=0.1, ax=axes[0])
axes[0].set_title("Raw Knowledge Graph\n(Unstructured)", fontsize=12)
axes[0].axis('off')
# Plot 2: Leaf Communities (High Resolution)
plot_graph_partition(axes[1], G, dict_leaf, "Level 1: Leaf Communities\n(Granular / Local Search)", pos)
# Plot 3: Root Communities (Low Resolution)
plot_graph_partition(axes[2], G, dict_root, "Level 0: Root Communities\n(Global / Map-Reduce)", pos)
plt.tight_layout()
plt.savefig("leiden_knowledge_graph_demo.png", dpi=600)
plt.savefig("leiden_knowledge_graph_demo.pdf")
plt.show()
if __name__ == "__main__":
run_leiden_demo()